
Partition regular
Encyclopedia
In mathematics
, the notion of partition regularity in combinatorics
is one approach to explaining when a set system is quite large.
Given a set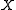 , a collection of subsets
, a collection of subsets 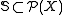 is called partition regular if every set A in the collection has the property that, no matter how A is partitioned into finitely many subsets, at least one of the subsets will also belong to the collection. That is,
is called partition regular if every set A in the collection has the property that, no matter how A is partitioned into finitely many subsets, at least one of the subsets will also belong to the collection. That is,
for any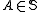 , and any finite partition
, and any finite partition 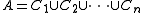 , there exists an i ≤ n, such that
, there exists an i ≤ n, such that 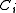 belongs to
belongs to 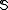 . Ramsey theory
. Ramsey theory
is sometimes characterized as the study of which collections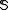 are partition regular.
are partition regular.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of partition regularity in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
is one approach to explaining when a set system is quite large.
Given a set
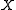 , a collection of subsets
, a collection of subsets 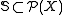 is called partition regular if every set A in the collection has the property that, no matter how A is partitioned into finitely many subsets, at least one of the subsets will also belong to the collection. That is,
is called partition regular if every set A in the collection has the property that, no matter how A is partitioned into finitely many subsets, at least one of the subsets will also belong to the collection. That is,for any
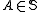 , and any finite partition
, and any finite partition 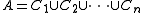 , there exists an i ≤ n, such that
, there exists an i ≤ n, such that 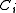 belongs to
belongs to 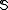 . Ramsey theory
. Ramsey theoryRamsey theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
is sometimes characterized as the study of which collections
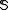 are partition regular.
are partition regular.Examples
- the collection of all infinite subsets of an infinite set X is a prototypical example. In this case partition regularity asserts that every finite partition of an infinite set has an infinite cell (i.e. the infinite pigeonhole principle.)
- sets with positive upper density in
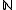 : the upper density
: the upper density 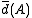 of
of 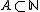 is defined as
is defined as 
- For any ultrafilterUltrafilterIn the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
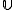 on a set
on a set 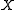 ,
, 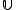 is partition regular. If
is partition regular. If 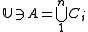 , then for exactly one
, then for exactly one 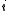 is
is 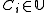 .
.
- sets of recurrence: a set R of integers is called a set of recurrence if for any measure preserving transformation
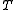 of the probability space (Ω, β, μ) and
of the probability space (Ω, β, μ) and 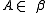 of positive measure there is a nonzero
of positive measure there is a nonzero 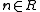 so that
so that 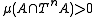 .
.
- Call a subset of natural numbers a.p.-rich if it contains arbitrarily long arithmetic progressions. Then the collection of a.p.-rich subsets is partition regular (Van der Waerden, 1927).
- Let
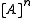 be the set of all n-subsets of
be the set of all n-subsets of 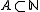 . Let
. Let 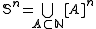 . For each n,
. For each n, 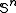 is partition regular. (RamseyRamsey's theoremIn combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
is partition regular. (RamseyRamsey's theoremIn combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
, 1930).
- For each infinite cardinal
 , the collection of stationary setStationary setIn mathematics, particularly in set theory and model theory, there are at least three notions of stationary set:-Classical notion:If \kappa \, is a cardinal of uncountable cofinality, S \subseteq \kappa \,, and S \, intersects every club set in \kappa \,, then S \, is called a stationary set....
, the collection of stationary setStationary setIn mathematics, particularly in set theory and model theory, there are at least three notions of stationary set:-Classical notion:If \kappa \, is a cardinal of uncountable cofinality, S \subseteq \kappa \,, and S \, intersects every club set in \kappa \,, then S \, is called a stationary set....
s of is partition regular. More is true: if
is partition regular. More is true: if 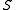 is stationary and
is stationary and 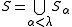 for some
for some 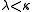 , then some
, then some 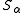 is stationary.
is stationary.
- the collection of
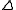 -sets:
-sets: 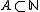 is a
is a 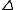 -set if
-set if 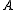 contains the set of differences
contains the set of differences 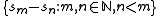 for some sequence
for some sequence 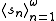 .
.
- the set of barriers on
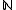 : call a collection
: call a collection 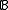 of finite subsets of
of finite subsets of 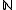 a barrier if:
a barrier if:
-
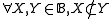 and
and - for all infinite
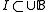 , there is some
, there is some 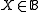 such that the elements of X are the smallest elements of I; i.e.
such that the elements of X are the smallest elements of I; i.e. 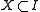 and
and 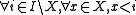 .
.
-
- This generalizes Ramsey's theoremRamsey's theoremIn combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
, as each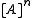 is a barrier. (Nash-WilliamsCrispin St. J. A. Nash-WilliamsCrispin St. John Alvah Nash-Williams was a British and Canadian mathematician. His research interest was in the field of discrete mathematics, especially graph theory....
is a barrier. (Nash-WilliamsCrispin St. J. A. Nash-WilliamsCrispin St. John Alvah Nash-Williams was a British and Canadian mathematician. His research interest was in the field of discrete mathematics, especially graph theory....
, 1965)
- finite products of infinite trees (Halpern–Läuchli, 1966)
- piecewise syndetic sets (Brown, 1968)
- Call a subset of natural numbers i.p.-rich if it contains arbitrarily large finite sets together with all their finite sums. Then the collection of i.p.-rich subsets is partition regular (FolkmanJon FolkmanJon Hal Folkman was an American mathematician, a student of John Milnor, and a researcher at the RAND Corporation.-Schooling:Folkman was a Putnam Fellow in 1960. He received his Ph.D...
–RadoRichard RadoRichard Rado FRS was a Jewish German mathematician. He earned two Ph.D.s: in 1933 from the University of Berlin, and in 1935 from the University of Cambridge. He was interviewed in Berlin by Lord Cherwell for a scholarship given by the chemist Sir Robert Mond which provided financial support to...
–Sanders, 1968).
- (m, p, c)-sets (Deuber, 1973)
- IP setIP setIn mathematics, an IP set is a set of natural numbers which contains all finite sums of some infinite set.The finite sums of a set D of natural numbers are all those numbers that can be obtained by adding up the elements of some finite nonempty subset of D.The set of all finite sums over D is often...
s (Hindman, 1974, see also Hindman, Strauss, 1998)
- MTk sets for each k, i.e. k-tuples of finite sums (Milliken–Taylor, 1975)
- central sets; i.e. the members of any minimal idempotent in
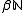 , the Stone–Čech compactificationStone–Cech compactificationIn the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
, the Stone–Čech compactificationStone–Cech compactificationIn the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
of the integers. (Furstenberg, 1981, see also Hindman, Strauss, 1998)

