IP set
Encyclopedia
In mathematics
, an IP set is a set of natural number
s which contains all finite sums of some infinite set.
The finite sums of a set D of natural numbers are all those numbers that can be obtained by adding up the elements of some finite nonempty subset of D.
The set of all finite sums over D is often denoted as FS(D).
A set A of natural numbers is an IP set if there exists an infinite set D such that FS(D) is a subset of A.
Some authors give a slightly different definition of IP sets. They require that FS(D) equal A instead of just being a subset.
Sources disagree on the origin of the name IP set. Some claim it was coined by Furstenberg and Weiss to abbreviate "Infinite-dimensional Parallelepiped
", others that it abbreviates "idempotent" (since a set is IP if and only if it is a member of an idempotent ultrafilter
).
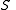is an IP set and 
, then at least one 
is an IP set.
This is known as Hindman's Theorem, or the Finite Sums Theorem.
Since the set of natural numbers itself is an IP-set and partitions can also be seen as colorings,
we can reformulate a special case of Hindman's Theorem in more familiar terms: Suppose the natural numbers are "colored" with n different colors; each natural number gets one and only one of the n colors. Then there exists a color c and an infinite set D of natural numbers, all colored with c, such that every finite sum over D also has color c.
Hindman's Theorem states that the class of IP sets is partition regular.
s and partial semigroups in general.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an IP set is a set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s which contains all finite sums of some infinite set.
The finite sums of a set D of natural numbers are all those numbers that can be obtained by adding up the elements of some finite nonempty subset of D.
The set of all finite sums over D is often denoted as FS(D).
A set A of natural numbers is an IP set if there exists an infinite set D such that FS(D) is a subset of A.
Some authors give a slightly different definition of IP sets. They require that FS(D) equal A instead of just being a subset.
Sources disagree on the origin of the name IP set. Some claim it was coined by Furstenberg and Weiss to abbreviate "Infinite-dimensional Parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
", others that it abbreviates "idempotent" (since a set is IP if and only if it is a member of an idempotent ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
).
Hindman's Theorem
If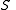 is an IP set and , then at least one is an IP set.This is known as Hindman's Theorem, or the Finite Sums Theorem.
Since the set of natural numbers itself is an IP-set and partitions can also be seen as colorings,
we can reformulate a special case of Hindman's Theorem in more familiar terms: Suppose the natural numbers are "colored" with n different colors; each natural number gets one and only one of the n colors. Then there exists a color c and an infinite set D of natural numbers, all colored with c, such that every finite sum over D also has color c.
Hindman's Theorem states that the class of IP sets is partition regular.
Semigroups
The definition of being IP has been extended from subsets of the special semigroup of natural numbers with addition to subsets of semigroupSemigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s and partial semigroups in general.
See also
- Syndetic setSyndetic setIn mathematics, a syndetic set is a subset of the natural numbers, having the property of "bounded gaps": that the sizes of the gaps in the sequence of natural numbers is bounded.-Definition:...
- Piecewise syndetic set
- Thick set
- Ergodic Ramsey theoryErgodic Ramsey theoryErgodic Ramsey theory is a branch of mathematics where problems motivated by additive combinatorics are proven using ergodic theory.Ergodic Ramsey theory arose shortly after Endre Szemerédi's proof that a set of positive upper density contains arbitrarily long arithmetic progressions, when Hillel...