
Piecewise syndetic set
Encyclopedia
In mathematics
, piecewise syndeticity is a notion of largeness of subsets of the natural number
s.
Let denote the set of finite subsets of
denote the set of finite subsets of 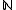 . Then a set
. Then a set 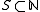 is called piecewise syndetic if there exists
is called piecewise syndetic if there exists 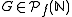 such that for every
such that for every 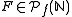 there exists an
there exists an  such that
such that
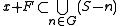
where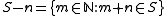 . Informally, S is piecewise syndetic if S contains arbitrarily long intervals with gaps bounded by some fixed bound b.
. Informally, S is piecewise syndetic if S contains arbitrarily long intervals with gaps bounded by some fixed bound b.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, piecewise syndeticity is a notion of largeness of subsets of the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s.
Let
 denote the set of finite subsets of
denote the set of finite subsets of 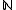 . Then a set
. Then a set 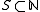 is called piecewise syndetic if there exists
is called piecewise syndetic if there exists 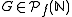 such that for every
such that for every 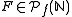 there exists an
there exists an  such that
such that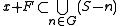
where
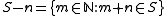 . Informally, S is piecewise syndetic if S contains arbitrarily long intervals with gaps bounded by some fixed bound b.
. Informally, S is piecewise syndetic if S contains arbitrarily long intervals with gaps bounded by some fixed bound b.Properties
- A set is piecewise syndetic if and only if it is the intersection of a syndetic setSyndetic setIn mathematics, a syndetic set is a subset of the natural numbers, having the property of "bounded gaps": that the sizes of the gaps in the sequence of natural numbers is bounded.-Definition:...
and a thick set.
- If S is piecewise syndetic then S contains arbitrarily long arithmetic progressions.
- A set S is piecewise syndetic if and only if there exists some ultrafilter U which contains S and U is in the smallest two-sided ideal of
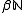 , the Stone–Čech compactificationStone–Cech compactificationIn the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
, the Stone–Čech compactificationStone–Cech compactificationIn the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
of the natural numbers.
- Partition regularity: if
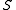 is piecewise syndetic and
is piecewise syndetic and 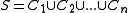 , then for some
, then for some 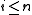 ,
, 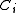 contains a piecewise syndetic set. (Brown, 1968)
contains a piecewise syndetic set. (Brown, 1968)
- If A and B are subsets of
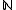 , and A and B have positive upper Banach densityNatural densityIn number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
, and A and B have positive upper Banach densityNatural densityIn number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
, then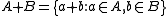 is piecewise syndetic
is piecewise syndetic
Other Notions of Largeness
There are many alternative definitions of largeness that also usefully distinguish subsets of natural numbers:- cofiniteCofiniteIn mathematics, a cofinite subset of a set X is a subset A whose complement in X is a finite set. In other words, A contains all but finitely many elements of X...
- positive upper density
- syndeticSyndetic setIn mathematics, a syndetic set is a subset of the natural numbers, having the property of "bounded gaps": that the sizes of the gaps in the sequence of natural numbers is bounded.-Definition:...
- thick
- member of a nonprincipal ultrafilterUltrafilterIn the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
- IP setIP setIn mathematics, an IP set is a set of natural numbers which contains all finite sums of some infinite set.The finite sums of a set D of natural numbers are all those numbers that can be obtained by adding up the elements of some finite nonempty subset of D.The set of all finite sums over D is often...

