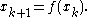Minimum polynomial extrapolation
Encyclopedia
In mathematics
, minimum polynomial extrapolation is a sequence transformation used for convergence acceleration.
While Aitken's method is the most famous, it often fails for vector sequences. An effective method for vector sequences is the minimum polynomial extrapolation. It is usually phrased in terms of the fixed point iteration:
Given iterates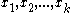
in 
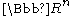, one constructs the 
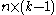matrix 
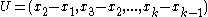whose columns are the 
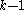differences. Then, one computes the vector 
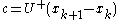where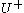 
denotes the Moore–Penrose pseudoinverse
of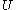
. The number 1 is then appended to the end of 
, and the extrapolated limit is
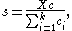
where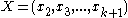
is the matrix whose columns are the 
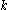iterates starting at 2.
The following 4 line MATLAB code segment implements the MPE algorithm:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, minimum polynomial extrapolation is a sequence transformation used for convergence acceleration.
While Aitken's method is the most famous, it often fails for vector sequences. An effective method for vector sequences is the minimum polynomial extrapolation. It is usually phrased in terms of the fixed point iteration:
Given iterates
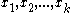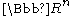in , one constructs the 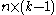matrix 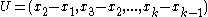whose columns are the 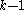differences. Then, one computes the vector 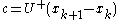where 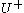denotes the Moore–Penrose pseudoinversePseudoinverse
In mathematics, and in particular linear algebra, a pseudoinverse of a matrix is a generalization of the inverse matrix. The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951 and...
of
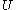. The number 1 is then appended to the end of , and the extrapolated limit is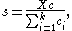where
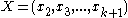is the matrix whose columns are the 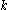iterates starting at 2.The following 4 line MATLAB code segment implements the MPE algorithm:
U=x(:,2:end-1)-x(:,1:end-2);
c=-pinv(U)*(x(:,end)-x(:,end-1));
c(end+1,1)=1;
s=(x(:,2:end)*c)/sum(c);