
Minkowski's bound
Encyclopedia
In algebraic number theory
, Minkowski's bound gives an upper bound
of the norm of ideals to be checked in order to determine the class number
of a number field K. It is named for the mathematician Hermann Minkowski
.
Let D be the discriminant
of the field, n be the degree of K over , and
, and 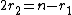 be the number of complex embeddings where
be the number of complex embeddings where 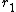 is the number of real embeddings. Then every class in the ideal class group
is the number of real embeddings. Then every class in the ideal class group
of K contains an integral ideal of norm
not exceeding Minkowski's bound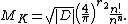
In particular, the class group is generated by the prime ideal
s of norm at most .
.
The result is a consequence of Minkowski's theorem
.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, Minkowski's bound gives an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
of the norm of ideals to be checked in order to determine the class number
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of a number field K. It is named for the mathematician Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
.
Let D be the discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of the field, n be the degree of K over
 , and
, and 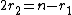 be the number of complex embeddings where
be the number of complex embeddings where 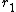 is the number of real embeddings. Then every class in the ideal class group
is the number of real embeddings. Then every class in the ideal class groupIdeal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of K contains an integral ideal of norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
not exceeding Minkowski's bound
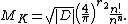
In particular, the class group is generated by the prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s of norm at most
 .
.The result is a consequence of Minkowski's theorem
Minkowski's theorem
In mathematics, Minkowski's theorem is the statement that any convex set in Rn which is symmetric with respect to the origin and with volume greater than 2n d contains a non-zero lattice point...
.

