Minkowski's question mark function
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Minkowski question mark function, sometimes called the slippery devil's staircase and denoted by
?(x), is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
possessing various unusual fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
properties, defined by Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
in 1904. It maps quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
s to rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s on the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
, via an expression relating the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansions of the quadratics to the binary expansions of the rationals, given by Arnaud Denjoy
Arnaud Denjoy
Arnaud Denjoy was a French mathematician.Denjoy was born in Auch, Gers. His contributions include work in harmonic analysis and differential equations. His integral was the first to be able to integrate all derivatives...
in 1938. In addition, it maps rational numbers to dyadic rational
Dyadic rational
In mathematics, a dyadic fraction or dyadic rational is a rational number whose denominator is a power of two, i.e., a number of the form a/2b where a is an integer and b is a natural number; for example, 1/2 or 3/8, but not 1/3...
s, as can be seen by a recursive definition closely related to the Stern-Brocot tree
Stern-Brocot tree
In number theory, the Stern–Brocot tree is an infinite complete binary tree in which the vertices correspond precisely to the positive rational numbers, whose values are ordered from left to right as in a search tree....
.
Definition
If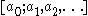
is the continued fraction representationContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
of an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
x, then
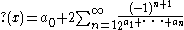
whereas:
If
is a continued fraction representation of a rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
x, then
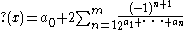
Intuitive explanation
To get some intuition for the definition above,consider the different ways
of interpreting an infinite string of bits beginning with 0 as a real number in [0,1].
One obvious way to interpret such a string is to place a binary point after the first 0 and read the string as a binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
expansion: thus, for instance, the string 001001001001001001001001...
represents the binary number 0.010010010010..., or 2/7. Another interpretation
views a string as the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
[0;a1,a2,...], where the integers ai are the run lengths in a run-length encoding
Run-length encoding
Run-length encoding is a very simple form of data compression in which runs of data are stored as a single data value and count, rather than as the original run...
of the string. The same example string 001001001001001001001001... then
corresponds to [0;2,1,2,1,2,1,...] = (√3-1)/2. (If the string ends in an infinitely long run of the same bit, we ignore it and terminate the representation; this is suggested by the formal "identity" [0;a1,...,an,∞]=[0;a1,...,an+1/∞]=
[0;a1,...,an+0]=[0;a1,...,an].)
The effect of the question mark function on [0,1] can then be understood as mapping the second interpretation of a string to the first interpretation of the same string, just as the Cantor function
Cantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
can be understood as mapping a triadic base 3 representation to a base 2 representation. Our example string gives the equality
Recursive definition for rational arguments
For rational numbers in the unit interval, the function may also be defined recursivelyRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
; if p/q and r/s are reduced fractions such that |ps − rq| = 1 (so that they are adjacent elements of a row of the Farey sequence
Farey sequence
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
) then
Using the base cases
it is then possible to compute ?(x) for any rational x, starting with the Farey sequence
Farey sequence
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
of order 2, then 3, etc.
If
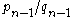and 
are two successive convergents of a continued fractionContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
, then the matrix
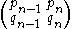
has determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
±1. Such a matrix is an element of
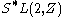, the group of two-by-two matrices with determinant ±1. This group is related to the modular groupModular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
.
Algorithm
This recursive definition naturally lends itself to an algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for computing the function to any desired degree of accuracy for any real number, as the following C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
function demonstrates. The algorithm descends the Stern-Brocot tree
Stern-Brocot tree
In number theory, the Stern–Brocot tree is an infinite complete binary tree in which the vertices correspond precisely to the positive rational numbers, whose values are ordered from left to right as in a search tree....
in search of the input x, and sums the terms of the binary expansion of
on the way. As long as the loop invariantLoop invariant
In computer science, a loop invariant is an invariant used to prove properties of loops. Informally, a loop invariant is a statement of the conditions that should be true on entry into a loop and that are guaranteed to remain true on every iteration of the loop...
remains satisfied there is no need to reduce the fraction 
since it is already in lowest terms. Another invariant is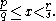 
The for loop in this program may be analyzed somewhat like a while loop, with the conditional break statements in the first three lines making out the condition. The only statements in the loop that can possibly affect the invariants are in the last two lines, and these can be shown to preserve the truth of both invariants as long as the first three lines have executed successfully without breaking out of the loop. A third invariant for the body of the loop (up to floating point precision) is 
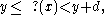but since d is halved at the beginning of the loop before any conditions are tested, our conclusion is only that 
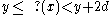at the termination of the loop.To prove termination
Loop variant
In computer science, a loop variant is a mathematical function defined on the state space of a computer program whose value is monotonically decreased with respect to a well-founded relation by the iteration of a while loop under some invariant conditions, thereby ensuring its termination...
, it is sufficient to note that the sum
increases by at least 1 with every iteration of the loop, and that the loop will terminate when this sum is too large to be represented in the primitive C data type long. However, in practice, the conditional break when "y+dy" is what ensures the termination of the loop in a reasonable amount of time./* Minkowski's question mark function */
double minkowski(double x) {
long p=x; if ((double)p>x) --p; /* p=floor(x) */
long q=1, r=p+1, s=1, m, n;
double d=1, y=p;
if (x<(double)p||(p<0)^(r<=0)) return x; /* out of range ?(x) =~ x */
for /* invariants: q*r-p*s1 && (double)p/q <= x && x < (double)r/s */
{
d/=2; if (y+dy) break; /* reached max possible precision */
m=p+r; if ((m<0)^(p<0)) break; /* sum overflowed */
n=q+s; if (n<0) break; /* sum overflowed */
if (x<(double)m/n) r=m, s=n;
else y+=d, p=m, q=n;
}
return y+d; /* final round-off */
}
Self-symmetry
The question mark is clearly visually self-similar. A monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
of self-similarities may be generated by the operators S and R, where S shrinks the question mark to half its size:
and R is the reflection:
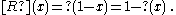
Both identities hold for all
. These may be repeatedly combined, forming a monoid. A general element of the monoid is then
for positive integers
. Each such element describes a self-similarity of the question mark function. This monoid is sometimes called the period-doubling monoid, and all period-doubling fractal curves have a self-symmetry described by it (the de Rham curveDe Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.The Cantor function, Césaro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve and the Koch curve are all special cases of the general de Rham...
, of which the question mark is a special case, is a category of such curves). Note also that the elements of the monoid are in correspondence with the rationals, by means of the identification of
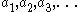with the continued fraction 
. Since both
and
are linear fractional transformations with integer coefficients, the monoid may be regarded as a subset of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
PSL(2,Z).
Properties of ?(x)
The question mark function is a strictly increasing and continuous, but not absolutely continuous function. The derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
vanishes on the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. There are several constructions for a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
that, when integrated, yields the question mark function. One such construction is obtained by measuring the density of the Farey numbers
Farey sequence
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
on the real number line. The question mark measure is the prototypical example of what are sometimes referred to as multi-fractal measures.
The question mark function sends rational numbers to dyadic rational number
Dyadic rational
In mathematics, a dyadic fraction or dyadic rational is a rational number whose denominator is a power of two, i.e., a number of the form a/2b where a is an integer and b is a natural number; for example, 1/2 or 3/8, but not 1/3...
s, meaning those whose base two
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
representation terminates, as may be proven by induction from the recursive construction outlined above. It sends quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
s to non-dyadic rational numbers. It is an odd function, and satisfies the functional equation ?(x + 1) = ?(x) + 1; consequently x→?(x) − x is an odd periodic function with period one. If ?(x) is irrational, then x is either algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
of degree greater than two, or transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
.
The Minkowski question mark function is a special case of fractal curves known as de Rham curve
De Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.The Cantor function, Césaro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve and the Koch curve are all special cases of the general de Rham...
s.
Conway box function
The ? is invertible, and the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
has also attracted the attention of various mathematicians, in particular John Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
, who discovered it independently, and whose notation for ?−1(x) is x with a box drawn around it (
). For technical reasons, this is instead denoted here by □(x). The box function can be computed as an encoding of the base two
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
expansion of
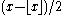, where 
denotes the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
. To the right of the decimal point, this will have n1 0s, followed by n2 1s, then n3 0s and so on. For
,
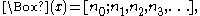
where the term on the right is a continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
.
Historical references