
Missionaries and cannibals problem
Encyclopedia
The missionaries and cannibals problem, and the closely related jealous husbands problem, are classic river-crossing problems. The missionaries and cannibals problem is a well-known toy problem
in artificial intelligence
, where it was used by Saul Amarel
as an example of problem representation.
In the jealous husbands problem, the missionaries and cannibals become three married couples, with the constraint that no woman can be in the presence of another man unless her husband is also present. Under this constraint, there cannot be both women and men present on a bank with women outnumbering men, since if there were, some woman would be husbandless. Therefore, upon changing women to cannibals and men to missionaries, any solution to the jealous husbands problem will also become a solution to the missionaries and cannibals problem.
. The vector's elements represent the number of missionaries on the wrong side, the number of cannibals on the wrong side, and the number of boats on the wrong side, respectively. Since the boat and all of the missionaries and cannibals start on the wrong side, the vector is initialized to <3,3,1>. Actions are represented using vector subtraction/addition to manipulate the state vector. For instance, if a lone cannibal crossed the river, the vector <0,1,1> would be subtracted from the state to yield <3,2,0>. The state would reflect that there are still three missionaries and two cannibals on the wrong side, and that the boat is now on the opposite bank. To fully solve the problem, a simple tree is formed with the initial state as the root. The five possible actions (<1,0,1>, <2,0,1>, <0,1,1>, <0,2,1>, and <1,1,1>) are then subtracted from the initial state, with the result forming children nodes of the root. Any node that has more cannibals than missionaries on either bank is in an invalid state, and is therefore removed from further consideration. The valid children nodes generated would be <3,2,0>, <3,1,0>, and <2,2,0>. For each of these remaining nodes, children nodes are generated by adding each of the possible action vectors. The algorithm continues alternating subtraction and addition for each level of the tree until a node is generated with the vector <0,0,0> as its value. This is the goal state, and the path from the root of the tree to this node represents a sequence of actions that solves the problem.
 (male) and a (female),
(male) and a (female), 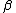 and b, and
and b, and 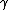 and c., p. 291.
and c., p. 291.
This is a shortest solution to the problem, but is not the only shortest solution., p. 291.
If however, only one man can get out of the boat at a time and husbands must be on the shore to count as with his wife as opposed to just being in the boat at the shore: move 5 to 6 is impossible, for as soon as has stepped out b on the shore won't be with her husband, despite him being just in the boat.
has stepped out b on the shore won't be with her husband, despite him being just in the boat.
As mentioned previously, this solution to the jealous husbands problem will become a solution to the missionaries and cannibals problem upon replacing men by missionaries and women by cannibals. In this case we may neglect the individual identities of the missionaries and cannibals. The solution just given is still shortest, and is one of four shortest solutions.
If a woman in the boat at the shore (but not on the shore) counts as being by herself (i.e. not in the presence of any men on the shore), then this puzzle can be solved in 9 one-way trips:
If an island is added in the middle of the river, then any number of couples can cross using a two-person boat. If crossings from bank to bank are not allowed, then 8n−6 one-way trips are required to ferry n couples across the river;, p. 76 if they are allowed, then 4n+1 trips are required if n exceeds 4, although a minimal solution requires only 16 trips if n equals 4., p. 79. If the jealous couples are replaced by missionaries and cannibals, the number of trips required does not change if crossings from bank to bank are not allowed; if they are however the number of trips decreases to 4n−1, assuming that n is at least 3., p. 81.
, usually attributed to Alcuin
(died 804.) In Alcuin's formulation the couples are brothers and sisters, but the constraint is still the same—no woman can be in the company of another man unless her brother is present., p. 74. From the 13th to the 15th century, the problem became known throughout Northern Europe, with the couples now being husbands and wives., pp. 291–293. The problem was later put in the form of masters and valets; the formulation with missionaries and cannibals did not appear until the end of the 19th century., p. 81 Varying the number of couples and the size of the boat was considered at the beginning of the 16th century., p. 296. Cadet de Fontenay considered placing an island in the middle of the river in 1879; this variant of the problem, with a two-person boat, was completely solved by Ian Pressman and David Singmaster
in 1989.
Toy problem
In scientific disciplines, a toy problem is a problem that is not of immediate scientific interest, yet is used as an expository device to illustrate a trait that may be shared by other, more complicated, instances of the problem, or as a way to explain a particular, more general, problem solving...
in artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, where it was used by Saul Amarel
Saul Amarel
Saul Amarel was professor of computer science at Rutgers University, and best known for his pioneer work in Artificial Intelligence. He also had a distinguished career as a scientist, engineer, and teacher. He was a pioneering contributor to advanced computing and AI methodologies...
as an example of problem representation.
The problem
In the missionaries and cannibals problem, three missionaries and three cannibals must cross a river using a boat which can carry at most two people, under the constraint that, for both banks, if there are missionaries present on the bank, they cannot be outnumbered by cannibals (if they were, the cannibals would eat the missionaries.) The boat cannot cross the river by itself with no people on board.In the jealous husbands problem, the missionaries and cannibals become three married couples, with the constraint that no woman can be in the presence of another man unless her husband is also present. Under this constraint, there cannot be both women and men present on a bank with women outnumbering men, since if there were, some woman would be husbandless. Therefore, upon changing women to cannibals and men to missionaries, any solution to the jealous husbands problem will also become a solution to the missionaries and cannibals problem.
Solving
Amarel devised a system for solving the Missionaries and Cannibals problem whereby the current state is represented by a simple vectorSolution
The earliest solution known to the jealous husbands problem, using 11 one-way trips, is as follows. The married couples are represented as (male) and a (female),
(male) and a (female), 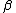 and b, and
and b, and 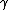 and c., p. 291.
and c., p. 291.| Trip number | Starting bank | Travel | Ending bank |
|---|---|---|---|
| (start) |  a a 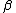 b b  c c |
||
| 1 | 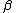 b b 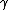 c c |
 a → a → |
|
| 2 | 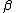 b b  c c |
← |
a |
| 3 |  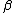 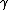 |
bc → | a |
| 4 |   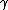 |
← a | b c |
| 5 |  a a |
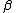 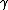 → → |
b c |
| 6 |  a a |
← 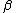 b b |
 c c |
| 7 | a b |  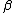 → → |
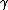 c c |
| 8 | a b | ← c |  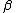 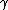 |
| 9 | b | a c → |  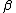 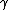 |
| 10 | b | ← 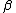 |
 a a 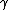 c c |
| 11 | 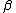 b → b → |
 a a 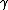 c c |
|
| (finish) |  a a 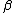 b b 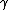 c c |
This is a shortest solution to the problem, but is not the only shortest solution., p. 291.
If however, only one man can get out of the boat at a time and husbands must be on the shore to count as with his wife as opposed to just being in the boat at the shore: move 5 to 6 is impossible, for as soon as
 has stepped out b on the shore won't be with her husband, despite him being just in the boat.
has stepped out b on the shore won't be with her husband, despite him being just in the boat.As mentioned previously, this solution to the jealous husbands problem will become a solution to the missionaries and cannibals problem upon replacing men by missionaries and women by cannibals. In this case we may neglect the individual identities of the missionaries and cannibals. The solution just given is still shortest, and is one of four shortest solutions.
If a woman in the boat at the shore (but not on the shore) counts as being by herself (i.e. not in the presence of any men on the shore), then this puzzle can be solved in 9 one-way trips:
| Trip number | Starting bank | Travel | Ending bank |
|---|---|---|---|
| (start) |  a a 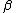 b b 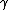 c c |
||
| 1 | 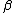 b b 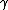 c c |
 a → a → |
|
| 2 | 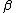 b b 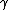 c c |
← a |  |
| 3 | 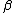 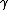 c c |
ab → |  |
| 4 | 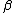  c c |
← b |  a a |
| 5 | 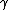 c c |
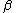 b → b → |
 a a |
| 6 | 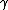 c c |
← b |  a a 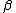 |
| 7 | 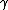 |
bc → |  a a 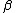 |
| 8 | 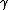 |
← c |  a a 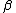 b b |
| 9 |  c → c → |
 a a 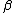 b b |
|
| (finish) |  a a 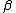 b b 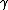 c c |
Variations
An obvious generalization is to vary the number of jealous couples (or missionaries and cannibals), the capacity of the boat, or both. If the boat holds 2 people, then 2 couples require 5 trips; with 4 or more couples, the problem has no solution. If the boat can hold 3 people, then up to 5 couples can cross; if the boat can hold 4 people, any number of couples can cross., p. 300.If an island is added in the middle of the river, then any number of couples can cross using a two-person boat. If crossings from bank to bank are not allowed, then 8n−6 one-way trips are required to ferry n couples across the river;, p. 76 if they are allowed, then 4n+1 trips are required if n exceeds 4, although a minimal solution requires only 16 trips if n equals 4., p. 79. If the jealous couples are replaced by missionaries and cannibals, the number of trips required does not change if crossings from bank to bank are not allowed; if they are however the number of trips decreases to 4n−1, assuming that n is at least 3., p. 81.
History
The first known appearance of the jealous husbands problem is in the medieval text Propositiones ad Acuendos JuvenesPropositiones ad Acuendos Juvenes
The medieval Latin manuscript Propositiones ad Acuendos Juvenes is one of the earliest known collections of recreational mathematics problems. The oldest known copy of the manuscript dates from the late 9th century. The text is attributed to Alcuin of York Some editions of the text contain 53...
, usually attributed to Alcuin
Alcuin
Alcuin of York or Ealhwine, nicknamed Albinus or Flaccus was an English scholar, ecclesiastic, poet and teacher from York, Northumbria. He was born around 735 and became the student of Archbishop Ecgbert at York...
(died 804.) In Alcuin's formulation the couples are brothers and sisters, but the constraint is still the same—no woman can be in the company of another man unless her brother is present., p. 74. From the 13th to the 15th century, the problem became known throughout Northern Europe, with the couples now being husbands and wives., pp. 291–293. The problem was later put in the form of masters and valets; the formulation with missionaries and cannibals did not appear until the end of the 19th century., p. 81 Varying the number of couples and the size of the boat was considered at the beginning of the 16th century., p. 296. Cadet de Fontenay considered placing an island in the middle of the river in 1879; this variant of the problem, with a two-person boat, was completely solved by Ian Pressman and David Singmaster
David Singmaster
David Breyer Singmaster is a retired professor of mathematics at London South Bank University, England, UK. A self-described metagrobologist, he is most famous for his solution to the Rubik's cube and his huge personal collection of mechanical puzzles and books of brain teasers. He is also...
in 1989.
See also
- Fox, goose and bag of beans puzzleFox, goose and bag of beans puzzleThe fox, goose and bag of beans puzzle is a river-crossing puzzle. It dates back to at least the 9th century, and has entered the folklore of a number of ethnic groups.-The story:...
- Transport puzzleTransport puzzleTransport puzzles are logistical puzzles, which often represent real-life transport problems.-Description:In transport puzzles you move persons and/or objects through a given landscape. As in rearrangement puzzles, no piece is ever lost or added to the board...
- Circumscription (logic)

