
Mitsuhiro Shishikura
Encyclopedia
is a Japan
ese mathematician
working in the field of complex dynamics
. He is currently professor at Kyoto University
in Japan.
Shishikura became internationally recognized for two of his earliest contributions, both of which solved long-standing open problems.
For his results, he was awarded the Salem Prize
in 1992, and the Iyanaga Spring Prize of the Mathematical Society of Japan
in 1995.
More recent results of Shishikura include
One of the main tools pioneered by Shishikura and used throughout his work is that of quasiconformal
surgery.
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
ese mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
working in the field of complex dynamics
Complex dynamics
Complex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
. He is currently professor at Kyoto University
Kyoto University
, or is a national university located in Kyoto, Japan. It is the second oldest Japanese university, and formerly one of Japan's Imperial Universities.- History :...
in Japan.
Shishikura became internationally recognized for two of his earliest contributions, both of which solved long-standing open problems.
- In his Master's thesis, he proved a conjectured of FatouPierre FatouPierre Joseph Louis Fatou was a French mathematician working in the field of complex analytic dynamics. He entered the École Normale Supérieure in Paris in 1898 to study mathematics and graduated in 1901 when he was appointed an astronomy post in the Paris Observatory...
from 1920 by showing that a rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of degree has at most
has at most 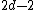 nonrepelling periodic cycles.
nonrepelling periodic cycles. - He proved that the boundary of the Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
has Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
two, confirming a conjecture stated by MandelbrotBenoît MandelbrotBenoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
and MilnorJohn MilnorJohn Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
.
For his results, he was awarded the Salem Prize
Salem Prize
The Salem Prize, founded by the widow of Raphael Salem, is awarded every year to a young mathematician judged to have done outstanding work in Salem's field of interest, primarily the theory of Fourier series.-Past winners:...
in 1992, and the Iyanaga Spring Prize of the Mathematical Society of Japan
Mathematical Society of Japan
The Mathematical Society of Japan was the first academic society in Japan.In 1877, the organization was establisehd as the Tokyo Sugaku Kaisha. It was re-organized and re-established in its present form in 1946....
in 1995.
More recent results of Shishikura include
- (in joint work with Kisaka) the existence of a transcendental entire functionEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
with a doubly connected wandering domain, answering a question of Baker from 1985; - (in joint work with Inou) a study of near-parabolic renormalization which is essential in Buff and Chéritat's recent proof of the existence of polynomial Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
s of positive planar Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
One of the main tools pioneered by Shishikura and used throughout his work is that of quasiconformal
Quasiconformal mapping
In mathematical complex analysis, a quasiconformal mapping, introduced by and named by , is a homeomorphism between plane domains which to first order takes small circles to small ellipses of bounded eccentricity....
surgery.
External links
- Faculty home page at Kyōto University

