In complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, a branch of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

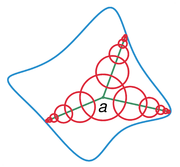
, the Mittag-Leffler star of a complex-analytic function

Holomorphic function

In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...

 is a set in the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

 obtained by attempting to extend that function along rays emanating from a given point. This concept is named after Gösta Mittag-Leffler.

Definition and elementary properties

Formally, the Mittag-Leffler star of a complex-analytic function ƒ defined on an open disk U in the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

 centered at a point a is the set of all points z in the complex plane such that ƒ can be continued analytically along the line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

 joining a and z (see analytic continuation along a curve).

It follows from the definition that the Mittag-Leffler star is an open star-convex set (with respect to the point a) and that it contains the disk U. Moreover, ƒ admits a single-valued analytic continuation

Analytic continuation

In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...

 to the Mittag-Leffler star.

Examples

• The Mittag-Leffler star of the complex exponential function
  Exponential function
  In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
  
   defined in a neighborhood of a = 0 is the entire complex plane.

• The Mittag-Leffler star of the complex logarithm
  Complex logarithm
  In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
  
   defined in the neighborhood of point a = 1 is the entire complex plane without the origin and the negative real axis. In general, given the complex logarithm defined in the neighborhood of a point a ≠ 0 in the complex plane, this function can be extended all the way to infinity on any ray starting at a, except on the ray which goes from a to the origin, one cannot extend the complex logarithm beyond the origin along that ray.

• Any open star-convex set is the Mittag-Leffler star of some complex-analytic function, since any open set in the complex plane is a domain of holomorphy
  Domain of holomorphy
  In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set....
  
  .

Uses

Any complex-analytic function ƒ defined around a point a in the complex plane can be expanded in a series

Series (mathematics)

A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....

 of polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

s which is convergent in the entire Mittag-Leffler star of ƒ at a. Each polynomial in this series is a linear combination of the first several terms in the Taylor series

Taylor series

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

 expansion of ƒ around a.

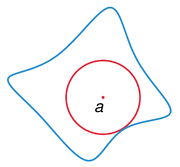
Such a series expansion of ƒ, called the Mittag-Leffler expansion, is convergent in a larger set than the Taylor series expansion of ƒ at  a. Indeed, the largest open set on which the latter series is convergent is a disk centered at a and contained within the Mittag-Leffler star of ƒ at a

External links

• Mittag-Leffler star at the Encyclopaedia of Mathematics
  Encyclopaedia of Mathematics
  The Encyclopaedia of Mathematics is a large reference work in mathematics. It is available in book form and on CD-ROM....