Modified nodal analysis
Encyclopedia
In Electrical Engineering
Modified Nodal Analysis or MNA is an extension of nodal analysis
which not only determines the circuit's node voltages (as in classical nodal analysis), but also some branch currents. Modified nodal analysis was developed as a formalism to mitigate the difficulty of representing voltage-defined components in nodal analysis (e.g. voltage-controlled voltage sources). It is one such formalism. Others, such as sparse tableau formulation, are equally general and related via matrix transformations.
- current
characteristic and the Kirchhoff's circuit laws
. According to the method is done in four steps, but it can be reduced to three.
Step 1
Write the KCL of the circuit. At each node of an electric circuit one writes the currents coming in and out of the node. Take care however in the MNA the current of the independent voltage sources is taken from the "plus" to the "minus". See Figure 1. Also note that the right hand side of each equation is always equal to zero. So that the branch currents that come inside the node are given a negative sign, whereas the branch currents coming out are given a positive sign.
Step 2
Use the BCE in terms of the node voltages of the circuit to eliminate as many branch currents as possible. Writing the BCE's in terms of the node voltages saves one step. If the BCE's were written in terms of the branch voltages, one more step, i.e., replacing the branches voltages for the node ones, would be necessary. In this article the letter "e" is use to name the node voltages, while the letter "v" is used to name the branch voltages.
Step 3
Finally, write down the unused equations.
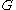i, 
, i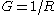s used instead of 
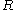. We now proceed as explained above.
Step 1
In this case there are two nodes,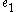
and 
. Also there are three currents: 
, 
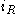and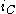 
.
At node e1 the KCL yields:
and at node e2:
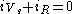
Step 2
With the provided BCEs in the table and observing that:
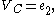
the following equations are result:
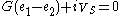
Step 3
Note that at this point there are two equations but three unknowns. The missing equation comes from the fact that
.
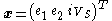is defined, then the above equations can be put in the form
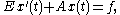
where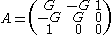
, 
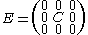and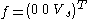 
.
This is a linear differential algebraic equation (DAE), since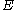
is singular. It can be proved that such a DAE coming from the Modified Nodal Analysis will have differentiation index less or equal than two.
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
Modified Nodal Analysis or MNA is an extension of nodal analysis
Nodal analysis
In electric circuits analysis, nodal analysis, node-voltage analysis, or the branch current method is a method of determining the voltage between "nodes" in an electrical circuit in terms of the branch currents.In analyzing a circuit using Kirchhoff's circuit laws, one can either do nodal...
which not only determines the circuit's node voltages (as in classical nodal analysis), but also some branch currents. Modified nodal analysis was developed as a formalism to mitigate the difficulty of representing voltage-defined components in nodal analysis (e.g. voltage-controlled voltage sources). It is one such formalism. Others, such as sparse tableau formulation, are equally general and related via matrix transformations.
Method
The MNA uses the element's Branch Constitutive Equations or BCE, i.e., their voltageVoltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
- current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
characteristic and the Kirchhoff's circuit laws
Kirchhoff's circuit laws
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
. According to the method is done in four steps, but it can be reduced to three.
Step 1
Write the KCL of the circuit. At each node of an electric circuit one writes the currents coming in and out of the node. Take care however in the MNA the current of the independent voltage sources is taken from the "plus" to the "minus". See Figure 1. Also note that the right hand side of each equation is always equal to zero. So that the branch currents that come inside the node are given a negative sign, whereas the branch currents coming out are given a positive sign.
Step 2
Use the BCE in terms of the node voltages of the circuit to eliminate as many branch currents as possible. Writing the BCE's in terms of the node voltages saves one step. If the BCE's were written in terms of the branch voltages, one more step, i.e., replacing the branches voltages for the node ones, would be necessary. In this article the letter "e" is use to name the node voltages, while the letter "v" is used to name the branch voltages.
Step 3
Finally, write down the unused equations.
Example
The figure shows a RC series circuit and the table shows the BCE of a linear resistor and a linear Capacitor. Note that in the case of the resistor the admittanceAdmittance
In electrical engineering, the admittance is a measure of how easily a circuit or device will allow a current to flow. It is defined as the inverse of the impedance . The SI unit of admittance is the siemens...
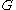i, 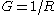, is used instead of 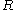. We now proceed as explained above.| Element | Branch equation |
|---|---|
| Resistor |  |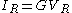
| Capacitor |  |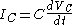
Step 1
In this case there are two nodes,
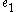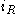and . Also there are three currents: , and 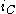.At node e1 the KCL yields:
and at node e2:
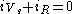
Step 2
With the provided BCEs in the table and observing that:
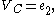
the following equations are result:
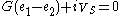
Step 3
Note that at this point there are two equations but three unknowns. The missing equation comes from the fact that
.Modified Nodal Analysis and DAEs
If the vector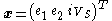 is defined, then the above equations can be put in the form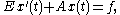where
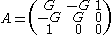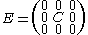, and 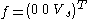.This is a linear differential algebraic equation (DAE), since
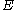is singular. It can be proved that such a DAE coming from the Modified Nodal Analysis will have differentiation index less or equal than two.