
Modular invariant of a group
Encyclopedia
In mathematics, a modular invariant of a group
is an invariant of a finite group
acting
on a vector space
of positive characteristic (usually dividing the order of the group). The study of modular invariants was originated in about 1914 by .
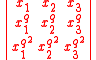
Then under the action of an element g of GLn(Fq) these determinants are all multiplied by det(g), so they are all invariants of SLn(Fp) and the ratio [e1, ...,en]/[0,1,...,n−1] are invariants of GLn(Fq), called Dickson invariants. Dickson proved that the full ring of invariants Fq[X1, ...,Xn]GLn(Fq) is a polynomial algebra over the n Dickson invariants [0,1,...,i−1,i+1,...,n]/[0,1,...,n−1] for i=0, 1, ..., n−1.
gave a shorter proof of Dickson's theorem.
The matrices [e1, ...,en] are divisible by all non-zero linear forms in the variables Xi with coefficients in the finite field Fq. In particular the Moore determinant [0,1,...,n−1] is a product of such linear forms, taken over 1+q+q2+...+qn–1 representatives of n–1 dimensional projective space over the field. This factorization is similar to the factorization of the Vandermonde determinant into linear factors.
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is an invariant of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of positive characteristic (usually dividing the order of the group). The study of modular invariants was originated in about 1914 by .
Dickson invariant
When G is the finite general linear group GLn(Fq) over the finite field Fq of order a prime power q acting on the ring Fq[X1, ...,Xn] in the natural way, found a complete set of invariants as follows. Write [e1, ...,en] for the determinant of the matrix whose entries are X, where e1, ...,en are non-negative integers. For example, the Moore determinant [0,1,2] of order 3 is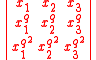
Then under the action of an element g of GLn(Fq) these determinants are all multiplied by det(g), so they are all invariants of SLn(Fp) and the ratio [e1, ...,en]/[0,1,...,n−1] are invariants of GLn(Fq), called Dickson invariants. Dickson proved that the full ring of invariants Fq[X1, ...,Xn]GLn(Fq) is a polynomial algebra over the n Dickson invariants [0,1,...,i−1,i+1,...,n]/[0,1,...,n−1] for i=0, 1, ..., n−1.
gave a shorter proof of Dickson's theorem.
The matrices [e1, ...,en] are divisible by all non-zero linear forms in the variables Xi with coefficients in the finite field Fq. In particular the Moore determinant [0,1,...,n−1] is a product of such linear forms, taken over 1+q+q2+...+qn–1 representatives of n–1 dimensional projective space over the field. This factorization is similar to the factorization of the Vandermonde determinant into linear factors.

