
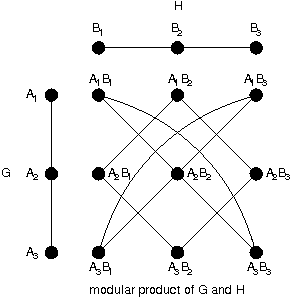
Modular product of graphs
Encyclopedia
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the modular product of graphs G and H is a graph such that
- the vertex set of the modular product of G and H is the cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
V(G) × V(H); and - any two vertices (u, v) and (u' , v' ) are adjacent in the modular product of G and H if and only if either
- u is adjacent with u' and v is adjacent with v' , or
- u is not adjacent with u' and v is not adjacent with v' .
Cliques in the modular product graph correspond to isomorphisms
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
of induced subgraphs of G and H. Therefore, the modular product graph can be used to reduce problems of induced subgraph isomorphism to problems of finding cliques
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
in graphs. Specifically, the largest graph that is an induced subgraph of both G and H corresponds to the maximum clique in their modular product. Although the problems of finding largest common induced subgraphs and of finding maximum cliques are both NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, this reduction allows clique-finding algorithms to be applied to the common subgraph problem.

