
Monge-Ampère equation
Encyclopedia
In mathematics
, a (real) Monge–Ampère equation is a nonlinear second order partial differential equation
of special kind. A second order equation for the unknown function u of two variables x,y is of Monge–Ampère type if it is linear in the determinant
of the Hessian matrix
of u and in the second order partial derivative
s of u. The independent variables (x,y) vary over a given domain D of R2. The term also applies to analogous equations with n independent variables. The most complete results so far have been obtained when the equation is elliptic
.
Monge–Ampère equations frequently arise in differential geometry, for example, in the Weyl
and Minkowski
problems in differential geometry of surfaces
. They were first studied by Gaspard Monge
in 1784 and later by André-Marie Ampère
in 1820. Important results in the theory of Monge–Ampère equations have been obtained by Sergei Bernstein, Aleksei Pogorelov
, Charles Fefferman
, and Louis Nirenberg
.
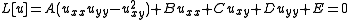
where A, B, C, D, and E are functions depending on the first order variables x, y, u, ux, and uy only.
to find u so that
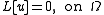
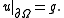
If
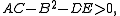
then the Dirichlet problem has at most one solution.
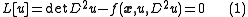
is a nonlinear elliptic partial differential equation (in the sense that its linearization
is uniformly elliptic), provided one confines attention to convex
solutions.
Accordingly, the operator L satisfies versions of the maximum principle
, and in particular solutions to the Dirichlet problem are unique, provided they exist.
, conformal geometry
, and CR geometry. One of the simplest of these applications is to the problem of prescribed Gauss curvature. Suppose that a real-valued function K is specified on a domain Ω in Rn, the problem of prescribed Gauss curvature seeks to identify a hypersurface of Rn+1 as a graph z=u(x) over x∈Ω so that, at each point of the surface the Gauss curvature is given by K(x). The resulting partial differential equation is
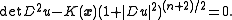
The Monge-Ampère equations are related to the Monge-Kantorovich optimal mass transportation problem, when the "cost functional" therein is given by the Euclidean distance.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a (real) Monge–Ampère equation is a nonlinear second order partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
of special kind. A second order equation for the unknown function u of two variables x,y is of Monge–Ampère type if it is linear in the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of u and in the second order partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of u. The independent variables (x,y) vary over a given domain D of R2. The term also applies to analogous equations with n independent variables. The most complete results so far have been obtained when the equation is elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
.
Monge–Ampère equations frequently arise in differential geometry, for example, in the Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
and Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
problems in differential geometry of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
. They were first studied by Gaspard Monge
Gaspard Monge
Gaspard Monge, Comte de Péluse was a French mathematician, revolutionary, and was inventor of descriptive geometry. During the French Revolution, he was involved in the complete reorganization of the educational system, founding the École Polytechnique...
in 1784 and later by André-Marie Ampère
André-Marie Ampère
André-Marie Ampère was a French physicist and mathematician who is generally regarded as one of the main discoverers of electromagnetism. The SI unit of measurement of electric current, the ampere, is named after him....
in 1820. Important results in the theory of Monge–Ampère equations have been obtained by Sergei Bernstein, Aleksei Pogorelov
Aleksei Pogorelov
Aleksei Vasil'evich Pogorelov , was a Soviet and Ukrainian mathematician. He was most famous for his contributions to convex and differential geometry...
, Charles Fefferman
Charles Fefferman
Charles Louis Fefferman is an American mathematician at Princeton University. His primary field of research is mathematical analysis....
, and Louis Nirenberg
Louis Nirenberg
Louis Nirenberg is a Canadian mathematician, and one of the outstanding analysts of the twentieth century. He has made fundamental contributions to linear and nonlinear partial differential equations and their application to complex analysis and geometry.He was born in Hamilton, Ontario and...
.
Description
Given two independent variables x and y, and one dependent variable u, the general Monge-Ampère equation is of the form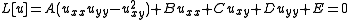
where A, B, C, D, and E are functions depending on the first order variables x, y, u, ux, and uy only.
Rellich's theorem
Let Ω be a bounded domain in R3, and suppose that on Ω A, B, C, D, and E are continuous functions of x and y only. Consider the Dirichlet problemDirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
to find u so that
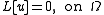
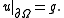
If
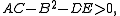
then the Dirichlet problem has at most one solution.
Ellipticity results
Suppose now that x is a variable with values in a domain in Rn, and that f(x,u,D2u) is a positive function. Then the Monge-Ampère equation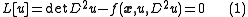
is a nonlinear elliptic partial differential equation (in the sense that its linearization
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
is uniformly elliptic), provided one confines attention to convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
solutions.
Accordingly, the operator L satisfies versions of the maximum principle
Maximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
, and in particular solutions to the Dirichlet problem are unique, provided they exist.
Applications
Monge–Ampère equations arise naturally in several problems in Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, conformal geometry
Conformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
, and CR geometry. One of the simplest of these applications is to the problem of prescribed Gauss curvature. Suppose that a real-valued function K is specified on a domain Ω in Rn, the problem of prescribed Gauss curvature seeks to identify a hypersurface of Rn+1 as a graph z=u(x) over x∈Ω so that, at each point of the surface the Gauss curvature is given by K(x). The resulting partial differential equation is
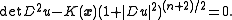
The Monge-Ampère equations are related to the Monge-Kantorovich optimal mass transportation problem, when the "cost functional" therein is given by the Euclidean distance.
Additional References
- Gilbarg, D. and Trudinger, N. S.Neil TrudingerNeil Sidney Trudinger is an Australian mathematician, known particularly for his work in the field of nonlinear elliptic partial differential equations....
Elliptic Partial Differential Equations of Second Order. Berlin: Springer-Verlag, 1983. ISBN 3540411607 ISBN 978-3540411604

