
Monomial basis
Encyclopedia
In mathematics
a monomial basis is a way to describe uniquely a polynomial
using a linear combination
of monomial
s. This description, the monomial form of a polynomial, is often used because of the simple structure of the monomial basis.
Polynomials in monomial form can be evaluated efficiently using the Horner algorithm.
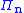 of polynomials with degree n is the polynomial sequence
of polynomials with degree n is the polynomial sequence
of monomials
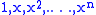
The monomial form of a polynomial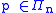 is a linear combination of monomials
is a linear combination of monomials

alternatively the shorter sigma notation can be used
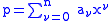
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a monomial basis is a way to describe uniquely a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
using a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s. This description, the monomial form of a polynomial, is often used because of the simple structure of the monomial basis.
Polynomials in monomial form can be evaluated efficiently using the Horner algorithm.
Definition
The monomial basis for the vector space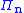 of polynomials with degree n is the polynomial sequence
of polynomials with degree n is the polynomial sequencePolynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
of monomials
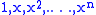
The monomial form of a polynomial
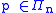 is a linear combination of monomials
is a linear combination of monomials
alternatively the shorter sigma notation can be used
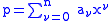
See also
- Polynomial sequencePolynomial sequenceIn mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
- Newton polynomialNewton polynomialIn the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is the interpolation polynomial for a given set of data points in the Newton form...
- Lagrange polynomialLagrange polynomialIn numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
- Legendre polynomial
- Bernstein form
- Chebyshev form

