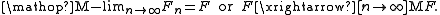In mathematical analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

, Mosco convergence, named for the Italian

Italy

Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...

 mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

 Umberto Mosco, is a notion of convergence for functionals

Functional (mathematics)

In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...

 that is used in nonlinear analysis and set-valued analysis. It is a particular case of Γ-convergence. Mosco convergence is sometimes phrased as “weak Γ-liminf and strong Γ-limsup” convergence since it uses both the weak and strong topologies on a a topological vector space

Topological vector space

In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...

 X.

Definition

Let X be a topological vector space and let X^∗ denote the dual space of continuous linear functionals on X. Let F_n : X → [0, +∞] be functionals on X for each n = 1, 2, ... The sequence (or, more generally, net) (F_n) is said to Mosco converge to another functional F : X → [0, +∞] if the following two conditions hold:

• lower bound inequality: for each sequence of elements x_n ∈ X converging weakly
  Weak convergence
  In mathematics, weak convergence may refer to:* The weak convergence of random variables of a probability distribution.* The weak convergence of a sequence of probability measures....
  
  to x ∈ X,

• upper bound inequality: for every x ∈ X there exists an approximating sequence of elements x_n ∈ X, converging strongly to x, such that

Since lower and upper bound inequalities of this type are used in the definition of Γ-convergence, Mosco convergence is sometimes phrased as “weak Γ-liminf and strong Γ-limsup” convergence. Mosco convergence is sometimes abbreviated to M-convergence and denoted by