In incidence geometry, the Moulton plane is an example of an affine plane

Affine plane (incidence geometry)

In incidence geometry, an affine plane is a system of points and lines that satisfy the following axioms :* Any two distinct points lie on a unique line.* Given a point and line there is a unique line which contains the point and is parallel to the line...

 in which Desargues' theorem

Desargues' theorem

In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...

 does not hold. It is named after the American astronomer Forest Ray Moulton

Forest Ray Moulton

Forest Ray Moulton was an American astronomer.He was born in Le Roy, Michigan, and was educated at Albion College. After graduating in 1894 , he performed his graduate studies at the University of Chicago and gained a Ph.D. in 1899...

. The points of the Moulton plane are simply the points in the real plane R² and the lines are the regular lines as well with the exception, that for lines with a negative slope

Slope

In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....

 the slope doubles when they pass the y-axis.

Formal definition

The Moulton plane is an incidence structure

Incidence structure

In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...

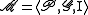, where 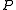denotes the set of points, 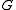the set of lines and 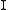the incidence relation "lies on":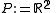



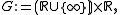
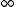is just a formal symbol for an element 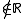. It is used to describe vertical lines, which you may think of as lines with an infinitely large slope.

The incidence relation is defined as follows:

For p = (x, y) ∈ P and g = (m, b) ∈ G we have

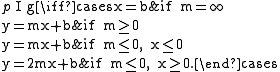
Application

The Moulton plane shows that affine planes in which Desargues' theorem does not hold do actually exist. As a consequence, the associated projective plane into which an affine plane can be extended, is non-desarguesian as well. Since in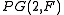 Desargues' theorem does hold, this means that there exist projective planes that are not isomorphic to 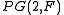. In other words not all projective planes can be described via the canonical construction (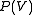) over a 3-dimensional vector space V.