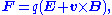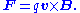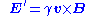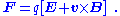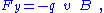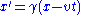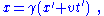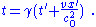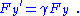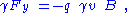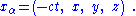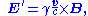Moving magnet and conductor problem - AbsoluteAstronomy.com

The moving magnet and conductor problem is a famous thought experiment

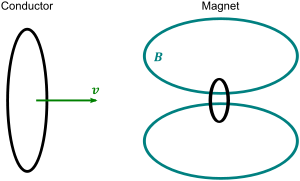
Thought experiment

A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...

, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity

Classical electromagnetism and special relativity

The theory of special relativity plays an important role in the modern theory of classical electromagnetism. First of all, it gives formulas for how electromagnetic objects, in particular the electric and magnetic fields, are altered under a Lorentz transformation from one inertial frame of...

. In it, the current in a conductor

Electrical conductor

In physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...

moving with constant velocity, v, with respect to a magnet

Magnet

A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...

is calculated in the frame of reference of the magnet and in the frame of reference of the conductor. The observable quantity in the experiment, the current, is the same in either case, in accordance with the basic principle of relativity, which states: "Only relative motion is observable; there is no absolute standard of rest". However, according to Maxwell's equations, the charges in the conductor experience a magnetic force in the frame of the magnet and an electric force in the frame of the conductor. The same phenomenon would seem to have two different descriptions depending on the frame of reference of the observer.

This problem, along with Michelson-Morley experiment

Michelson-Morley experiment

The Michelson–Morley experiment was performed in 1887 by Albert Michelson and Edward Morley at what is now Case Western Reserve University in Cleveland, Ohio. Its results are generally considered to be the first strong evidence against the theory of a luminiferous ether and in favor of special...

, formed the basis of Einstein's theory of relativity.

Introduction

Einstein's

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

1905 paper that introduced the world to relativity opens with a description of the magnet/conductor problem.http://www.fourmilab.ch/etexts/einstein/specrel/www/
An overriding requirement on the descriptions in different frameworks is that they be consistent

Consistency

Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...

. Consistency is an issue because Newtonian mechanics

Newton's laws of motion

Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...

predicts one transformation (so-called Galilean invariance

Galilean invariance

Galilean invariance or Galilean relativity is a principle of relativity which states that the fundamental laws of physics are the same in all inertial frames...

) for the forces that drive the charges and cause the current, while electrodynamics as expressed by Maxwell's equations

Maxwell's equations

Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...

predicts that the fields that give rise to these forces transform differently (according to Lorentz invariance). Observations of the aberration of light, culminating in the Michelson Morley experiment, established the validity of Lorentz invariance, and the development of special relativity

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

resolved the resulting disagreement with Newtonian mechanics. Special relativity revised the transformation of forces in moving reference frames to be consistent with Lorentz invariance. The details of these transformations are discussed below.

In addition to consistency, it would be nice to consolidate the descriptions so they appear to be frame-independent. A clue to a framework-independent description is the observation that magnetic fields in one reference frame become electric fields in another frame. Likewise, the solenoidal portion of electric fields (the portion that is not originated by electric charges) becomes a magnetic field in another frame: that is, the solenoidal electric fields and magnetic fields are aspects of the same thing. That means the paradox of different descriptions may be only semantic

Semantic gap

The semantic gap characterizes the difference between two descriptions of an object by different linguistic representations, for instance languages or symbols...

. A description that uses scalar and vector potentials φ and A instead of B and E avoids the semantical trap. A Lorentz-invariant four vector A^α = (φ / c₀, A ) replaces E and B and provides a frame-independent description (albeit less visceral than the E– B–description). An alternative unification of descriptions is to think of the physical entity as the electromagnetic field tensor, as described later on. This tensor contains both E and B fields as components, and has the same form in all frames of reference.

Background

Electromagnetic fields are not directly observable. The existence of classical

Classical physics

What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...

electromagnetic fields can be inferred from the motion of charged particles, whose trajectories are observable. Electromagnetic fields do explain the observed motions of classical charged particles.

A strong requirement in physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

is that all observers of the motion of a particle agree on the trajectory of the particle. For instance, if one observer notes that a particle collides with the center of a bullseye, then all observers must reach the same conclusion. This requirement places constraints on the nature of electromagnetic fields and on their transformation from one reference frame to another. It also places constraints on the manner in which fields affect the acceleration and, hence, the trajectories of charged particles.

Perhaps the simplest example, and one that Einstein referenced in his 1905 paper introducing special relativity

Special relativity

, is the problem of a conductor moving in the field of a magnet. In the frame of the magnet, a conductor experiences a magnetic force. In the frame of a conductor moving relative to the magnet, the conductor experiences a force due to an electric field. The magnetic field in the magnet frame and the electric field in the conductor frame must generate consistent results in the conductor. At the time of Einstein in 1905, the field equations as represented by Maxwell's equations

Maxwell's equations

were properly consistent. Newton's law of motion, however, had to be modified to provide consistent particle trajectories.

Transformation of fields, assuming Galilean transformations

Assuming that the magnet frame and the conductor frame are related by a Galilean transformation

Galilean transformation

The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...

, it is straightforward to compute the fields and forces in both frames. This will demonstrate that the induced current is indeed the same in both frames. As a byproduct, this argument will also yield a general formula for the electric and magnetic fields in one frame in terms of the fields in another frame.

In reality, the frames are not related by a Galilean transformation, but by a Lorentz transformation

Lorentz transformation

In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...

. Nevertheless, it will be a Galilean transformation to a very good approximation, at velocities much less than the speed of light.

Unprimed quantities correspond to the rest frame of the magnet, while primed quantities correspond to the rest frame of the conductor. Let v be the velocity of the conductor, as seen from the magnet frame.

Magnet frame

In the rest frame of the magnet, the magnetic field is some fixed field B(r), determined by the structure and shape of the magnet. The electric field is zero.

In general, the force exerted upon a particle of charge q in the conductor by the electric field

Electric field

In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...

and magnetic field

Magnetic field

A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...

is given by (SI units):

where

is the charge on the particle,

is the particle velocity and F is the Lorentz force

Lorentz force

In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...

. Here, however, the electric field is zero, so the force on the particle is

Conductor frame

In the conductor frame, the magnetic field B' will be related to the magnetic field B in the magnet frame according to: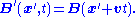

In this frame, there is an electric field, generated by the Maxwell-Faraday equation:

Using the above expression for B',

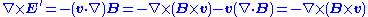
(using the chain rule

Chain rule

In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...

and Gauss's law for magnetism). This has the solution:

A charge q in the conductor will be at rest in the conductor frame. Therefore, the magnetic force term of the Lorentz force

Lorentz force

In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...

has no effect, and the force on the charge is given by

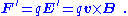
This demonstrates that the force is the same in both frames (as would be expected), and therefore any observable consequences of this force, such as the induced current, would also be the same in both frames. This is despite the fact that the force is seen to be an electric force in the conductor frame, but a magnetic force in the magnet's frame.

Galilean transformation formula for fields

A similar sort of argument can be made if the magnet's frame also contains electric fields. (The Ampere-Maxwell equation also comes into play, explaining how, in the conductor's frame, this moving electric field will contribute to the magnetic field.) The end result is that, in general,

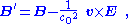
with c₀ the speed of light

Speed of light

The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

in free space.

By plugging these transformation rules into the full Maxwell's equations

Maxwell's equations

, it can be seen that if Maxwell's equations are true in one frame, then they are almost true in the other, but contain incorrect terms pro by the Lorentz transformation

Lorentz transformation

, and the field transformation equations also must be changed, according to the expressions given below.

Transformation of fields as predicted by Maxwell's equations

In a frame moving at velocity v, the E-field in the moving frame when there is no E-field in the stationary magnet frame Maxwell's equations transform as:

where

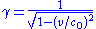
is called the Lorentz factor

Lorentz factor

The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...

and c₀ is the speed of light

Speed of light

in free space. This result is a consequence of requiring that observers in all inertial frames arrive at the same form for Maxwell's equations. In particular, all observers must see the same speed of light c₀. That requirement leads to the Lorentz transformation

Lorentz transformation

for space and time. Assuming a Lorentz transformation, invariance of Maxwell's equations then leads to the above transformation of the fields for this example.

Consequently, the force on the charge is

This expression differs from the expression obtained from the nonrelativistic Newton's law of motion by a factor of

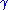. Special relativity modifies space and time in a manner such that the forces and fields transform consistently.

Modification of dynamics for consistency with Maxwell's equations

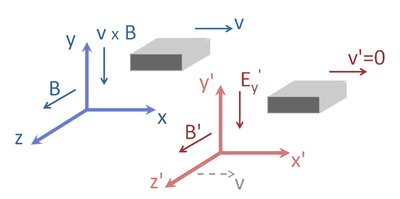
The Lorentz force has the same form in both frames, though the fields differ, namely:

See Figure 1. To simplify, let the magnetic field point in the z-direction and vary with location x, and let the conductor translate in the positive x-direction with velocity v. Consequently, in the magnet frame where the conductor is moving, the Lorentz force points in the negative y-direction, perpendicular to both the velocity, and the B-field. The force on a charge, here due only to the B-field, is

while in the conductor frame where the magnet is moving, the force is also in the negative y-direction, and now due only to the E-field with a value:

The two forces differ by the Lorentz factor γ. This difference is expected in a relativistic theory, however, due to the change in space-time between frames, as discussed next.

Relativity takes the Lorentz transformation of space-time suggested by invariance of Maxwell's equations and imposes it upon dynamics as well (a revision of Newton's laws of motion

Newton's laws of motion

Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...

). In this example, the Lorentz transformation affects the x-direction only (the relative motion of the two frames is along the x-direction). The relations connecting time and space are ( primes denote the moving conductor frame ) :

These transformations lead to a change in the y-component of a force:

That is, within Lorentz invariance, force is not the same in all frames of reference, unlike Galilean invariance. But, from the earlier analysis based upon the Lorentz force law:

which agrees completely. So the force on the charge is not the same in both frames, but it transforms as expected according to relativity.

Newton's law of motion in modern notation

The modern approach to obtaining the relativistic version of Newton's law of motion can be obtained by writing Maxwell's equations in covariant form

Covariant transformation

In physics, a covariant transformation is a rule , that describes how certain physical entities change under a change of coordinate system....

and identifying a covariant form that is a generalization of Newton's law of motion.

Newton's law of motion can be written in modern covariant notation in terms of the field strength tensor as (cgs units):

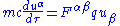
where m is the particle mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

, q is the charge

Electric charge

Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...

, and

is the 4-velocity

Four-velocity

In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...

of the particle. Here,

is c times the proper time

Proper time

In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...

of the particle and

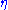is the Minkowski metric tensor.

The field strength tensor is written in terms of fields as:

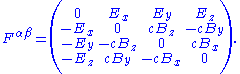
Alternatively, using the four vector:

related to the electric and magnetic fields by:

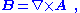
the field tensor becomes:

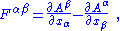
where:

The fields are transformed to a frame moving with constant relative velocity by:

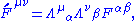
where

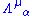is a Lorentz transformation

Lorentz transformation

.

In the magnet/conductor problem this gives

which agrees with the traditional transformation when one takes into account the difference between SI and cgs units. Thus, the relativistic modification to Newton's law of motion using the traditional Lorentz force yields predictions for the motion of particles that are consistent in all frames of reference with Maxwell's equations.

External links

Magnets and conductors in special relativity

Introduction

Background

Transformation of fields, assuming Galilean transformations

Magnet frame

Conductor frame

Galilean transformation formula for fields

Transformation of fields as predicted by Maxwell's equations

Modification of dynamics for consistency with Maxwell's equations

Newton's law of motion in modern notation

External links

Further reading

See also