In automata theory

Automata theory

In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...

, a Muller automaton is a type of an ω-automaton

Ω-automaton

In automata theory, a branch of theoretical computer science, an ω-automaton is a deterministic or nondeterministic automaton that runs on infinite, rather than finite, strings as input...

.
The acceptance condition separates a Muller automomaton from other ω-automata.
The Muller automata is defined using Muller acceptance condition, i.e. the set of all states visited infinitely often must be an element of the acceptance set. Both deterministic and non-deterministic Muller automata recognize the ω-regular languages.

Formal definition

Formally, a deterministic Muller-automaton is a tuple A = (Q,Σ,δ,q₀,F) that consists of the following information:

• Q is a finite set. The elements of Q are called the states of Q.
• Σ is a finite set called the alphabet of A.
• δ: Q × Σ → Q is a function, called the transition function of A.
• q₀ is an element of Q, called the initial state.
• F is set of sets of states. Formally, F ⊆ P(Q) where P(Q) is powerset of Q. F defines the acceptance condition.A accepts exactly those runs in which the set of infinitely often occurring states is an element of F

In a non-deterministic Muller automaton, the transition function δ is replaced with a transition relation Δ that returns a set of states and initial state is q₀ is replaced by a set of initial states Q₀. Generally, Muller automaton refers to non-deterministic Muller automaton.

For more comprehensive formalism look at ω-automaton

Ω-automaton

In automata theory, a branch of theoretical computer science, an ω-automaton is a deterministic or nondeterministic automaton that runs on infinite, rather than finite, strings as input...

.

Equivalence with other ω-automata

The Muller automata are equally expressive as parity automata, Rabin Automata, Streett automata, and non-deterministic Büchi automata

Büchi automaton

In computer science and automata theory, a Büchi automaton is a type of ω-automaton, which extends a finite automaton to infinite inputs. It accepts an infinite input sequence iff there exists a run of the automaton that visits one of the final states infinitely often. Büchi automata recognize the...

, to mention some, and strictly more expressive than the deterministic Büchi automata. The equivalence of the above automata and non-deterministic Muller automata can be shown very easily as the accepting conditions of these automata can be emulated using the acceptance condition of Muller automata. McNaughton's Theorem

McNaughton's Theorem

In automata theory, McNaughton's theorem refers to a theorem that asserts that the set of ω-regular languages is identical to the set of languages recognizable by deterministic Muller automata....

 demonstrates the equivalence of non-deterministic Büchi automaton and deterministic Muller automaton. Thus, deterministic and non-deterministic Muller automaton are equivalent in terms of the languages they can accept.

Transformation to non-deterministic muller automaton

Following is a list of automata construction

Automata construction

In automata theory, automata construction is an important mathematical technique used to demonstrate the existence of an automaton with a certain desired property...

s which transforms a type of ω-automata to a non-deterministic muller automaton.

From Büchi automaton

Büchi automaton

In computer science and automata theory, a Büchi automaton is a type of ω-automaton, which extends a finite automaton to infinite inputs. It accepts an infinite input sequence iff there exists a run of the automaton that visits one of the final states infinitely often. Büchi automata recognize the...

If is the set of final states in a Büchi automata with the set of states , we can construct a Muller automata with same set of states, transition function and initial state with the muller accepting condition as F = { X | X ∈ 2^Q ∧ X ∩ B ≠ }

From Rabin automaton/Parity automaton

Similarly, the Rabin conditions 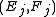can be emulated by constructing the acceptance set in the Muller automata as all sets in 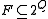which satisfy , for some j. Note that this covers the case of Parity automaton too, as the Parity acceptance condition can be expressed as Rabin acceptance condition easily.

From Streett automaton

The Streett conditions 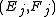can be emulated by constructing the acceptance set in the Muller automata as all sets in 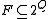which satisfy 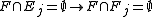, for all j.

Transformation to deterministic muller automaton

Union of two deterministic muller automaton

From Büchi automaton
McNaughton's Theorem

McNaughton's Theorem

In automata theory, McNaughton's theorem refers to a theorem that asserts that the set of ω-regular languages is identical to the set of languages recognizable by deterministic Muller automata....

provides a procedure to transform non-deterministic Büchi automaton to deterministic Muller automaton.