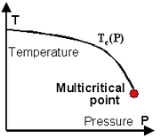
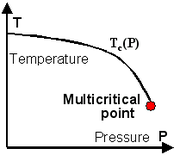
Multicritical point
Encyclopedia
Multicritical points are special points in the parameter space of thermodynamic or
other systems with a continuous phase transition
. At least two thermodynamic or other
parameters must be adjusted to reach a multicritical point. At a multicritical point the
system belongs to a universality class different from the "normal" universality class.
A more detailed definition requires concepts from the theory of critical phenomena
,
a branch of physics
that reached a very satisfying state in the 1970s.
called a critical manifold
.
 As an example consider a substance ferromagnetic below a
As an example consider a substance ferromagnetic below a
transition temperature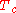 , and paramagnetic above
, and paramagnetic above 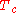 . The parameter space here is
. The parameter space here is
the temperature axis, and the critical manifold consists of the point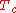 . Now add
. Now add
hydrostatic pressure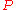 to the parameter space. Under hydrostatic pressure the substance
to the parameter space. Under hydrostatic pressure the substance
normally still becomes ferromagnetic below a temperature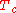 (
(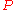 ).
).
This leads to a
critical curve in the ( ) plane - a
) plane - a  -dimensional critical manifold. Also taking into account
-dimensional critical manifold. Also taking into account
shear stress as a thermodynamic parameter leads to a critical surface
as a thermodynamic parameter leads to a critical surface  (
(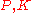 ) in the
) in the
(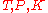 ) parameter space - a
) parameter space - a 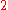 -dimensional critical manifold.
-dimensional critical manifold.
Critical manifolds of dimension and
and  may have physically reachable borders of dimension
may have physically reachable borders of dimension
 which in turn may have borders of dimension
which in turn may have borders of dimension  . The system still is critical at
. The system still is critical at
these borders. However, criticality terminates for good reason, and the points on the
borders normally belong to another universality class than the universality class realized
within the critical manifold. All the points on the border of a critical manifold are
multicritical points.
Instead of terminating somewhere critical manifolds also may branch or intersect.
The points on the intersections or branch lines also are multicritical points.
At least two parameters must be adjusted to reach a multicritical point.
A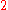 -dimensional critical manifold may have two
-dimensional critical manifold may have two 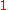 -dimensional borders intersecting at a point. Two parameters must be adjusted to reach such a border, three parameters must be adjusted to reach the intersection of the two borders. A system of this type represents up to four universality classes: one within the critical manifold, two on the borders and one on the intersection of the borders.
-dimensional borders intersecting at a point. Two parameters must be adjusted to reach such a border, three parameters must be adjusted to reach the intersection of the two borders. A system of this type represents up to four universality classes: one within the critical manifold, two on the borders and one on the intersection of the borders.
The gas-liquid critical point is not multicritical, because the phase transition at
the vapour pressure curve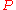 (
( ) is discontinuous and the critical manifold thus consists of a single point.
) is discontinuous and the critical manifold thus consists of a single point.
the parameters must be tuned in such a way that the renormalized counterpart of the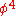 -term of the Hamiltonian vanishes.
-term of the Hamiltonian vanishes.
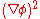 -term of the Hamiltonian vanishes.
-term of the Hamiltonian vanishes.
a Lifshitz tricritical point.
provides a detailed and quantitative explanation of critical phenomena.
other systems with a continuous phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
. At least two thermodynamic or other
parameters must be adjusted to reach a multicritical point. At a multicritical point the
system belongs to a universality class different from the "normal" universality class.
A more detailed definition requires concepts from the theory of critical phenomena
Critical phenomena
In physics, critical phenomena is the collective name associated with thephysics of critical points. Most of them stem from the divergence of thecorrelation length, but also the dynamics slows down...
,
a branch of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
that reached a very satisfying state in the 1970s.
Definition
The union of all the points of the parameter space for which the system is critical iscalled a critical manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.

transition temperature
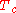 , and paramagnetic above
, and paramagnetic above 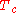 . The parameter space here is
. The parameter space here isthe temperature axis, and the critical manifold consists of the point
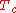 . Now add
. Now addhydrostatic pressure
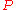 to the parameter space. Under hydrostatic pressure the substance
to the parameter space. Under hydrostatic pressure the substancenormally still becomes ferromagnetic below a temperature
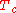 (
(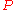 ).
).This leads to a
critical curve in the (
 ) plane - a
) plane - a  -dimensional critical manifold. Also taking into account
-dimensional critical manifold. Also taking into accountshear stress
 as a thermodynamic parameter leads to a critical surface
as a thermodynamic parameter leads to a critical surface  (
(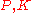 ) in the
) in the(
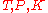 ) parameter space - a
) parameter space - a 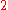 -dimensional critical manifold.
-dimensional critical manifold.Critical manifolds of dimension
 and
and  may have physically reachable borders of dimension
may have physically reachable borders of dimension which in turn may have borders of dimension
which in turn may have borders of dimension  . The system still is critical at
. The system still is critical atthese borders. However, criticality terminates for good reason, and the points on the
borders normally belong to another universality class than the universality class realized
within the critical manifold. All the points on the border of a critical manifold are
multicritical points.
Instead of terminating somewhere critical manifolds also may branch or intersect.
The points on the intersections or branch lines also are multicritical points.
At least two parameters must be adjusted to reach a multicritical point.
A
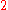 -dimensional critical manifold may have two
-dimensional critical manifold may have two 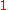 -dimensional borders intersecting at a point. Two parameters must be adjusted to reach such a border, three parameters must be adjusted to reach the intersection of the two borders. A system of this type represents up to four universality classes: one within the critical manifold, two on the borders and one on the intersection of the borders.
-dimensional borders intersecting at a point. Two parameters must be adjusted to reach such a border, three parameters must be adjusted to reach the intersection of the two borders. A system of this type represents up to four universality classes: one within the critical manifold, two on the borders and one on the intersection of the borders.The gas-liquid critical point is not multicritical, because the phase transition at
the vapour pressure curve
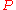 (
( ) is discontinuous and the critical manifold thus consists of a single point.
) is discontinuous and the critical manifold thus consists of a single point.Tricritical Point and Multicritical Points of Higher Order
To reach a tricritical pointTricritical point
In condensed matter physics, dealing with the macroscopic physical properties of matter, a tricritical point is a point in the phase diagram of a system at whichthree-phase coexistence terminates...
the parameters must be tuned in such a way that the renormalized counterpart of the
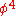 -term of the Hamiltonian vanishes.
-term of the Hamiltonian vanishes.Lifshitz Point
To reach a Lifshitz point the parameters must be tuned in such a way that the renormalized counterpart of the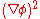 -term of the Hamiltonian vanishes.
-term of the Hamiltonian vanishes.Lifshitz Tricritical Point
This multicritical point is simultaneously tricritical and Lifshitz. Three parameters must be adjusted to reacha Lifshitz tricritical point.
Renormalization Group
The renormalization groupRenormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
provides a detailed and quantitative explanation of critical phenomena.

