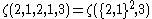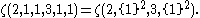Multiple zeta function
Encyclopedia
In mathematics
, the multiple zeta functions generalisations of the Riemann zeta function, defined by
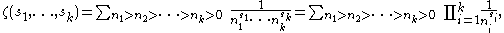
and converge when Re(s1)+...+Re(si) > i for all i. Like the Riemann zeta function, the multiple zeta functions can be analytically continued to be meromorphic functions (see, for example, Zhao (1999)). When s1, ..., si are all positive integers these sums are often called multiple zeta values (MZVs) or Euler sums.
The standard shorthand for writing multiple zeta functions is to place repeating strings of the argument within braces and use a superscript to indicate the number of repetitions. For example,
and
Multiple zeta functions are known to satisfy what is known as MZV duality, the simplest case of which is the famous identity of Euler
:
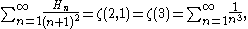
where Hn are the harmonic numbers.
Special values of double zeta functions:
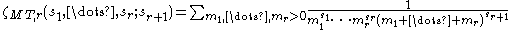
It is a special case of the Shintani zeta function
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the multiple zeta functions generalisations of the Riemann zeta function, defined by
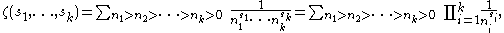
and converge when Re(s1)+...+Re(si) > i for all i. Like the Riemann zeta function, the multiple zeta functions can be analytically continued to be meromorphic functions (see, for example, Zhao (1999)). When s1, ..., si are all positive integers these sums are often called multiple zeta values (MZVs) or Euler sums.
The standard shorthand for writing multiple zeta functions is to place repeating strings of the argument within braces and use a superscript to indicate the number of repetitions. For example,
and
Multiple zeta functions are known to satisfy what is known as MZV duality, the simplest case of which is the famous identity of Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
:
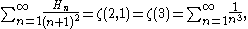
where Hn are the harmonic numbers.
Special values of double zeta functions:
Mordell-Tornheim zeta values
The Mordell-Tornheim zeta function, introduced by who was motivated by the papers and , is defined by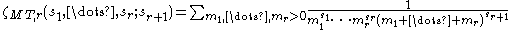
It is a special case of the Shintani zeta function
Shintani zeta function
In mathematics, a Shintani zeta function or Shintani L-function is a generalization of the Riemann zeta function. They were studied studied by...
.
External Links
- Lecture notes on the Multiple Zeta Function by Jonathan BorweinJonathan BorweinJonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H...
and Wadim ZudilinWadim ZudilinWadim Zudilin is a Russian number theorist who is active in studying hypergeometric functions and zeta constants. He studied under Yuri V. Nesterenko and worked at Moscow State University, the Steklov Institute of Mathematics and the Max Planck Institute for Mathematics. He now works at the...
.