Multiplication theorem
Encyclopedia
In mathematics
, the multiplication theorem is a certain type of identity obeyed by many special functions related to the gamma function
. For the explicit case of the gamma function, the identity is a product of values; thus the name. The various relations all stem from the same underlying principle; that is, the relation for one special function can be derived from that for the others, and is simply a manifestation of the same identity in different guises.
. For example, the multiplication theorem for the gamma function follows from the Chowla–Selberg formula, which follows from the theory of complex multiplication
. The infinite sums are much more common, and follow from characteristic zero relations on the hypergeometric series.
The following tabulates the various appearances of the multiplication theorem for finite characteristic; the characteristic zero relations are given further down. In all cases, n and k are non-negative integers. For the special case of n = 2, the theorem is commonly referred to as the duplication formula.
are the prototypical examples. The duplication formula for the gamma function is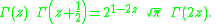
It is sometimes called the Legendre duplication formula or Legendre relation, in honor of Adrien-Marie Legendre
. The multiplication theorem is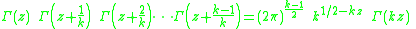
for integer k ≥ 1, and is sometimes called Gauss's multiplication formula, in honour of Carl Friedrich Gauss
. The multiplication theorem for the gamma functions can be understood to be a special case, for the trivial character, of the Chowla–Selberg formula.
of the gamma function, and thus, the multiplication theorem becomes additive, instead of multiplicative:
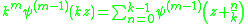
for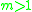
, and, for 
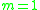, one has the digamma function:
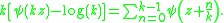
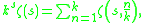
where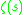
is the Riemann zeta function. This is a special case of
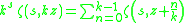
and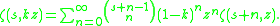
Multiplication formulas for the non-principal characters may be given in the form of Dirichlet L-functions.
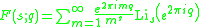
where Lis(z) is the polylogarithm. It obeys the duplication formula
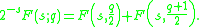
As such, it is an eigenvector of the Bernoulli operator with eigenvalue 2−s. The multiplication theorem is
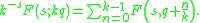
The periodic zeta function occurs in the reflection formula for the Hurwitz zeta function, which is why the relation that it obeys, and the Hurwitz zeta relation, differ by the interchange of s → −s.
The Bernoulli polynomials
may be obtained as a limiting case of the periodic zeta function, taking s to be an integer, and thus the multiplication theorem there can be derived from the above. Similarly, substituting q = log z leads to the multiplication theorem for the polylogarithm.
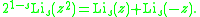
The general multiplication formula is in the form of a Gauss sum
or discrete Fourier transform
:
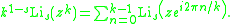
These identities follow from that on the periodic zeta function, taking z = log q.
is
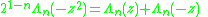
and thus resembles that for the polylogarithm, but twisted by i.
, the multiplication theorems were given by Joseph Ludwig Raabe
in 1851:
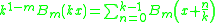
and for the Euler polynomials,
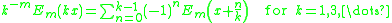
and
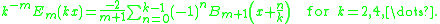
The Bernoulli polynomials may be obtained as a special case of the Hurwitz zeta function, and thus the identities follow from there.
:
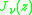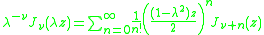
where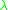
and 
may be taken as arbitrary complex numbers. Such characteristic-zero identities follow generally from one of many possible identities on the hypergeometric series.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the multiplication theorem is a certain type of identity obeyed by many special functions related to the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. For the explicit case of the gamma function, the identity is a product of values; thus the name. The various relations all stem from the same underlying principle; that is, the relation for one special function can be derived from that for the others, and is simply a manifestation of the same identity in different guises.
Finite characteristic
The multiplication theorem takes two common forms. In the first case, a finite number of terms are added or multiplied to give the relation. In the second case, an infinite number of terms are added or multiplied. The finite form typically occurs only for the gamma and related functions, for which the identity follows from a p-adic relation over a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. For example, the multiplication theorem for the gamma function follows from the Chowla–Selberg formula, which follows from the theory of complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
. The infinite sums are much more common, and follow from characteristic zero relations on the hypergeometric series.
The following tabulates the various appearances of the multiplication theorem for finite characteristic; the characteristic zero relations are given further down. In all cases, n and k are non-negative integers. For the special case of n = 2, the theorem is commonly referred to as the duplication formula.
Gamma function
The duplication formula and the multiplication theorem for the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
are the prototypical examples. The duplication formula for the gamma function is
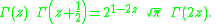
It is sometimes called the Legendre duplication formula or Legendre relation, in honor of Adrien-Marie Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
. The multiplication theorem is
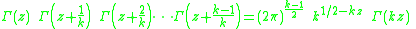
for integer k ≥ 1, and is sometimes called Gauss's multiplication formula, in honour of Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
. The multiplication theorem for the gamma functions can be understood to be a special case, for the trivial character, of the Chowla–Selberg formula.
Polygamma function
The polygamma function is the logarithmic derivativeLogarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
of the gamma function, and thus, the multiplication theorem becomes additive, instead of multiplicative:
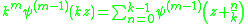
for
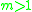, and, for 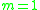, one has the digamma function: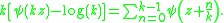Hurwitz zeta function
For the Hurwitz zeta function generalizes the polygamma function to non-integer orders, and thus obeys a very similar multiplication theorem: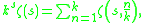where
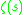is the Riemann zeta function. This is a special case of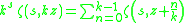and
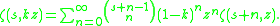
Multiplication formulas for the non-principal characters may be given in the form of Dirichlet L-functions.
Periodic zeta function
The periodic zeta function is sometimes defined as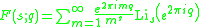where Lis(z) is the polylogarithm. It obeys the duplication formula
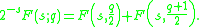
As such, it is an eigenvector of the Bernoulli operator with eigenvalue 2−s. The multiplication theorem is
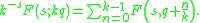
The periodic zeta function occurs in the reflection formula for the Hurwitz zeta function, which is why the relation that it obeys, and the Hurwitz zeta relation, differ by the interchange of s → −s.
The Bernoulli polynomials
Bernoulli polynomials
In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
may be obtained as a limiting case of the periodic zeta function, taking s to be an integer, and thus the multiplication theorem there can be derived from the above. Similarly, substituting q = log z leads to the multiplication theorem for the polylogarithm.
Polylogarithm
The duplication formula takes the form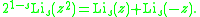The general multiplication formula is in the form of a Gauss sum
Gauss sum
In mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
or discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
:
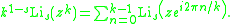
These identities follow from that on the periodic zeta function, taking z = log q.
Kummer's function
The duplication formula for Kummer's functionKummer's function
In mathematics, there are several functions known as Kummer's function. One is known as the confluent hypergeometric function of Kummer. Another one, defined below, is related to the polylogarithm...
is
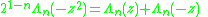
and thus resembles that for the polylogarithm, but twisted by i.
Bernoulli polynomials
For the Bernoulli polynomialsBernoulli polynomials
In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
, the multiplication theorems were given by Joseph Ludwig Raabe
Joseph Ludwig Raabe
Joseph Ludwig Raabe was a Swiss mathematician.-Life:As his parents were quite poor, Raabe was forced to earn his living from a very early age by giving private lessons. He began to study mathematics in 1820 at the Polytechnicum in Vienna, Austria...
in 1851:
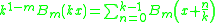
and for the Euler polynomials,
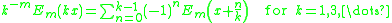
and
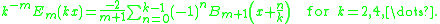
The Bernoulli polynomials may be obtained as a special case of the Hurwitz zeta function, and thus the identities follow from there.
Characteristic zero
The multiplication theorem over a field of characteristic zero does not close after a finite number of terms, but requires an infinite series to be expressed. Examples include that for the Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
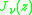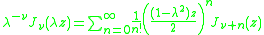
:where
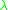and may be taken as arbitrary complex numbers. Such characteristic-zero identities follow generally from one of many possible identities on the hypergeometric series.