
Multiplicity-one theorem
Encyclopedia
In the mathematical theory of automorphic representations, a multiplicity-one theorem is a result about the representation theory
of an adelic
reductive algebraic group. The multiplicity in question is the number of times a given abstract group representation
is realised in a certain space, of square integrable functions, given in a concrete way.
s of K. Let Z denote the centre of G and let ω be a continuous unitary character
from Z(K)\Z(A)× to C×. Let L20(G(K)/G(A), ω) denote the space of cusp forms with central character ω
on G(A). This space decomposes into a direct sum of Hilbert spaces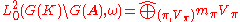
where the sum is over irreducible subrepresentations and mπ are non-negative integer
s.
The group of adelic points of G, G(A), is said to satisfy the multiplicity-one property if any smooth irreducible admissible representation
of G(A) occurs with multiplicity at most one in the space of cusp form
s of central character ω, i.e. mπ is 0 or 1 for all such π.
, GL(n), has the multiplicity-one property was proved by for n = 2 and independently by and for n > 2 using the uniqueness of the Whittaker model
. Multiplicity-one also holds for SL(2)
, but not for SL(n) for n > 2 .
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of an adelic
Adelic algebraic group
In abstract algebra, an adelic algebraic group is a topological group defined by an algebraic group G over a number field K, and the adele ring A = A of K. It consists of the points of G having values in A; the definition of the appropriate topology is straightforward only in case G is a linear...
reductive algebraic group. The multiplicity in question is the number of times a given abstract group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
is realised in a certain space, of square integrable functions, given in a concrete way.
Definition
Let G be a reductive algebraic group over a number field K and let A denote the adeleAdele
Adele is a female given name of European origin used in English, French, German and Italian with a meaning of noble, kind, and tender...
s of K. Let Z denote the centre of G and let ω be a continuous unitary character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
from Z(K)\Z(A)× to C×. Let L20(G(K)/G(A), ω) denote the space of cusp forms with central character ω
Cuspidal representation
In number theory, cuspidal representations are certain representations of algebraic groups that occur discretely in L^2 spaces. The term cuspidal is derived, at a certain distance, from the cusp forms of classical modular form theory...
on G(A). This space decomposes into a direct sum of Hilbert spaces
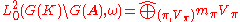
where the sum is over irreducible subrepresentations and mπ are non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
The group of adelic points of G, G(A), is said to satisfy the multiplicity-one property if any smooth irreducible admissible representation
Admissible representation
In mathematics, admissible representations are a well-behaved class of representations used in the representation theory of reductive Lie groups and locally compact totally disconnected groups. They were introduced by Harish-Chandra....
of G(A) occurs with multiplicity at most one in the space of cusp form
Cusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
s of central character ω, i.e. mπ is 0 or 1 for all such π.
Results
The fact that the general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
, GL(n), has the multiplicity-one property was proved by for n = 2 and independently by and for n > 2 using the uniqueness of the Whittaker model
Whittaker model
In representation theory, a branch of mathematics, the Whittaker model is a realization of a representation of a reductive algebraic group such as GL2 over a finite or local or global field on a space of functions on the group. It is named after E. T...
. Multiplicity-one also holds for SL(2)
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
, but not for SL(n) for n > 2 .

