
Multitree
Encyclopedia
In combinatorics
and order-theoretic
mathematics, a multitree may describe either of two equivalent structures: a directed acyclic graph
in which the set of nodes reachable from any node form a tree
, or a partially ordered set
(also called a diamond-free poset) that does not have four items a, b, c, and d forming a diamond suborder with and but with b and c incomparable to each other.
relation in G forms a diamond-free partial order. Conversely, if P is a diamond-free partial order, its transitive reduction
forms a DAG in which the successors of any node form a tree.
is a family F of sets whose inclusion ordering forms a diamond-free poset. If D(n) denotes the largest possible diamond-free family of subsets of an n-element set, then it is known that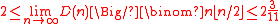
and it is conjectured that the limit is 2.
over the same ground set. If a family tree
may contain multiple marriages from one family to another, but does not contain marriages between any two blood relatives, then it forms a multitree. In the context of computational complexity theory
, multitrees have also been called strongly unambiguous graphs or mangroves; they can be used to model nondeterministic algorithm
s in which there is at most one computational path connecting any two states.
, a directed acyclic graph
formed by assigning an orientation to each edge of an undirected tree
, may be viewed as a special case of a multitree.
The word "multitree" has also been used to refer to a series-parallel partial order
, or to other structures formed by combining multiple trees.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and order-theoretic
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
mathematics, a multitree may describe either of two equivalent structures: a directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
in which the set of nodes reachable from any node form a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, or a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
(also called a diamond-free poset) that does not have four items a, b, c, and d forming a diamond suborder with and but with b and c incomparable to each other.
Equivalence between DAG and poset definitions
If G is a directed acyclic graph in which the nodes reachable from each vertex form a tree (or equivalently, if G is a directed graph in which there is at most one directed path between any two nodes, in either direction) then the reachabilityReachability
In graph theory, reachability is the notion of being able to get from one vertex in a directed graph to some other vertex. Note that reachability in undirected graphs is trivial — it is sufficient to find the connected components in the graph, which can be done in linear time.- Definition :For a...
relation in G forms a diamond-free partial order. Conversely, if P is a diamond-free partial order, its transitive reduction
Transitive reduction
In mathematics, a transitive reduction of a binary relation R on a set X is a minimal relation R' on X such that the transitive closure of R' is the same as the transitive closure of R. If the transitive closure of R is antisymmetric and finite, then R' is unique...
forms a DAG in which the successors of any node form a tree.
Diamond-free families
A diamond-free family of setsFamily of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
is a family F of sets whose inclusion ordering forms a diamond-free poset. If D(n) denotes the largest possible diamond-free family of subsets of an n-element set, then it is known that
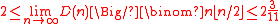
and it is conjectured that the limit is 2.
Applications
Multitrees may be used to represent multiple overlapping taxonomiesTaxonomy
Taxonomy is the science of identifying and naming species, and arranging them into a classification. The field of taxonomy, sometimes referred to as "biological taxonomy", revolves around the description and use of taxonomic units, known as taxa...
over the same ground set. If a family tree
Family tree
A family tree, or pedigree chart, is a chart representing family relationships in a conventional tree structure. The more detailed family trees used in medicine, genealogy, and social work are known as genograms.-Family tree representations:...
may contain multiple marriages from one family to another, but does not contain marriages between any two blood relatives, then it forms a multitree. In the context of computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, multitrees have also been called strongly unambiguous graphs or mangroves; they can be used to model nondeterministic algorithm
Nondeterministic algorithm
In computer science, a nondeterministic algorithm is an algorithm that can exhibit different behaviors on different runs, as opposed to a deterministic algorithm. There are several ways an algorithm may behave differently from run to run. A concurrent algorithm can perform differently on different...
s in which there is at most one computational path connecting any two states.
Related structures
A polytreePolytree
In graph theory, a polytree is a directed graph with at most one undirected path between any two vertices. In other words, a polytree is a directed acyclic graph for which there are no undirected cycles either...
, a directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
formed by assigning an orientation to each edge of an undirected tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, may be viewed as a special case of a multitree.
The word "multitree" has also been used to refer to a series-parallel partial order
Series-parallel partial order
In order-theoretic mathematics, a series-parallel partial order is a partially ordered set built up from smaller series-parallel partial orders by two simple composition operations....
, or to other structures formed by combining multiple trees.

