
Müntz–Szász theorem
Encyclopedia
The Müntz–Szász theorem is a basic result of approximation theory
, proved by Herman Müntz
in 1914 and Otto Szász
(1884–1952) in 1916. Roughly speaking, the theorem shows to what extent the Weierstrass theorem on polynomial approximation can have holes dug into it, by restricting certain coefficients in the polynomials to be zero. The form of the result had been conjectured by Sergei Bernstein before it was proved.
The theorem, in a special case, states that a necessary and sufficient condition for the monomial
s
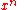
to span a dense subset of the Banach space
C[a,b] of all continuous function
s with complex number
values on the closed interval [a,b] with a > 0, with the uniform norm, when the n form a subset S of the natural number
s, is that the sum
of the reciprocals, taken over S, should diverge. For an interval [0, b], the constant function
s are necessary: assuming therefore that 0 is in S, the condition on the other exponents is as before.
More generally, one can take exponents from any strictly increasing sequence of positive real numbers, and the same result holds. Szász showed that for complex number exponents, the same condition applied to the sequence of real parts.
There are also versions for the Lp spaces
.
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
, proved by Herman Müntz
Herman Müntz
Herman Müntz was a German mathematician, now remembered for the Müntz approximation theorem....
in 1914 and Otto Szász
Otto Szász
Otto Szász was a Hungarian mathematician who worked on real analysis, in particular on Fourier series. He proved the Müntz–Szász theorem and introduced the Szász–Mirakyan operator...
(1884–1952) in 1916. Roughly speaking, the theorem shows to what extent the Weierstrass theorem on polynomial approximation can have holes dug into it, by restricting certain coefficients in the polynomials to be zero. The form of the result had been conjectured by Sergei Bernstein before it was proved.
The theorem, in a special case, states that a necessary and sufficient condition for the monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s
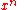
to span a dense subset of the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
C[a,b] of all continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s with complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
values on the closed interval [a,b] with a > 0, with the uniform norm, when the n form a subset S of the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, is that the sum
- Σ n−1
of the reciprocals, taken over S, should diverge. For an interval [0, b], the constant function
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
s are necessary: assuming therefore that 0 is in S, the condition on the other exponents is as before.
More generally, one can take exponents from any strictly increasing sequence of positive real numbers, and the same result holds. Szász showed that for complex number exponents, the same condition applied to the sequence of real parts.
There are also versions for the Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.

