
Nahm equations
Encyclopedia
The Nahm equations are a system of ordinary differential equation
s introduced by Werner Nahm in the context of the Nahm transform – an alternative to Ward
's twistor construction of monopoles
. The Nahm equations are formally analogous to the algebraic equations in the ADHM construction
of instanton
s, where finite order matrices are replaced by differential operators.
Deep study of the Nahm equations was carried out by Nigel Hitchin
and Simon Donaldson
. Conceptually, the equations arise in the process of infinite-dimensional hyperkähler reduction. Among their many applications we can mention: Hitchin's construction of monopoles, where this approach is critical for establishing nonsingularity of monopole solutions; Donaldson's description of the moduli space
of monopoles; and the existence of hyperkähler structure
on coadjoint orbits of complex semisimple Lie groups, proved by Peter Kronheimer, Olivier Biquard, and A.G. Kovalev.
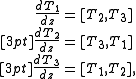
together with certain analyticity properties, reality conditions, and boundary conditions. The three equations can be written concisely using the Levi-Civita symbol
, in the form
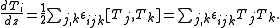
More generally, instead of considering N by N matrices, one can consider Nahm's equations with values in a Lie algebra g.
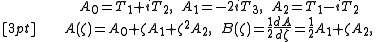
then the system of Nahm equations is equivalent to the Lax equation

As an immediate corollary, we obtain that the spectrum of the matrix A does not depend on z. Therefore, the characteristic equation
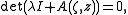
which determines the so-called spectral curve in the twistor space TP1, is invariant under the flow in z.
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s introduced by Werner Nahm in the context of the Nahm transform – an alternative to Ward
Richard S. Ward
Richard Samuel Ward FRS is a professor of mathematics at Durham University. He is most famous for his extension of Roger Penrose's twistor theory to nonlinear cases...
's twistor construction of monopoles
Monopole (mathematics)
In mathematics, a monopole is a connection over a principal bundle G with a section of the associated adjoint bundle. The connection and Higgs field should satisfy the Bogomolnyi equation and be of finite action....
. The Nahm equations are formally analogous to the algebraic equations in the ADHM construction
ADHM construction
The ADHM construction or monad construction is the construction of all instantons using method of linear algebra by Michael Atiyah, Vladimir G. Drinfel'd, Nigel. J. Hitchin, Yuri I...
of instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
s, where finite order matrices are replaced by differential operators.
Deep study of the Nahm equations was carried out by Nigel Hitchin
Nigel Hitchin
Nigel Hitchin is a British mathematician working in the fields of differential geometry, algebraic geometry, and mathematical physics.-Academic career:...
and Simon Donaldson
Simon Donaldson
Simon Kirwan Donaldson FRS , is an English mathematician known for his work on the topology of smooth four-dimensional manifolds. He is now Royal Society research professor in Pure Mathematics and President of the Institute for Mathematical Science at Imperial College London...
. Conceptually, the equations arise in the process of infinite-dimensional hyperkähler reduction. Among their many applications we can mention: Hitchin's construction of monopoles, where this approach is critical for establishing nonsingularity of monopole solutions; Donaldson's description of the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of monopoles; and the existence of hyperkähler structure
Hyperkähler manifold
In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...
on coadjoint orbits of complex semisimple Lie groups, proved by Peter Kronheimer, Olivier Biquard, and A.G. Kovalev.
Equations
Let T1(z),T2(z), T3(z) be three matrix-valued meromorphic functions of a complex variable z. The Nahm equations are a system of matrix differential equations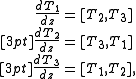
together with certain analyticity properties, reality conditions, and boundary conditions. The three equations can be written concisely using the Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
, in the form
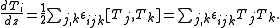
More generally, instead of considering N by N matrices, one can consider Nahm's equations with values in a Lie algebra g.
Additional conditions
The variable z is restricted to the open interval (0,2), and the following conditions are imposed:-
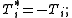
-
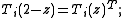
- Ti can be continued to a meromorphic function of z in a neighborhood of the closed interval [0,2], analytic outside of 0 and 2, and with simple poles at z = 0 and z = 2; and
- At the poles, the residues of (T1,T2, T3) form an irreducible representation of the group SU(2).
Nahm–Hitchin description of monopoles
There is a natural equivalence between- the monopoles of charge k for the group SU(2), modulo gauge transformations, and
- the solutions of Nahm equations satisfying the additional conditions above, modulo the simultaneous conjugation of T1,T2, T3 by the group O(k,R).
Lax representation
The Nahm equations can be written in the Lax form as follows. Set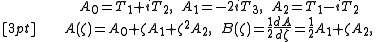
then the system of Nahm equations is equivalent to the Lax equation

As an immediate corollary, we obtain that the spectrum of the matrix A does not depend on z. Therefore, the characteristic equation
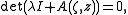
which determines the so-called spectral curve in the twistor space TP1, is invariant under the flow in z.
External links
- Islands project – a wiki about the Nahm equations and related topics

