Nesbitt's inequality
Encyclopedia
In mathematics
, Nesbitt's inequality is a special case of the Shapiro inequality
. It states that for positive real numbers a, b and c we have: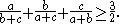
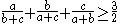
we transform the left hand side: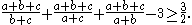
Now this can be transformed into: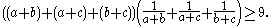
Division by 3 and the right factor yields: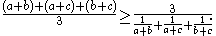
Now on the left we have the arithmetic mean
and on the right the harmonic mean
, so this inequality is true.
We might also want to try to use GM for three variables.
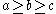, we have that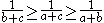
define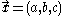
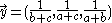
The scalar product of the two sequences is maximum because of the Rearrangement inequality if they are arranged the same way, call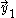
and 
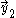the vector 
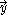shifted by one and by two, we have: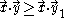
Addition yields Nesbitt's inequality.
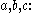
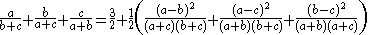
This clearly proves that the left side is no less than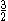
for positive a,b and c.
Note: every rational inequality can be solved by transforming it to the appropriate identity, see Hilbert's seventeenth problem
.
We add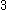
to both sides.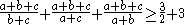
Now this can be transformed into: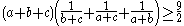
Multiply by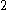
on both sides.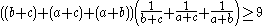
Which is true by the Cauchy-Schwarz inequality.
,
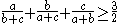we substitute a+b=x, b+c=y, c+a=z.
Now, we get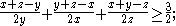
this can be transformed to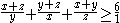
which is true, by inequality of arithmetic and geometric means
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Nesbitt's inequality is a special case of the Shapiro inequality
Shapiro inequality
In mathematics, the Shapiro inequality is an inequality proposed by H. Shapiro in 1954.-Statement of the inequality:Suppose n is a natural number and x_1, x_2, \dots, x_n are positive numbers and:* n is even and less than or equal to 12, or...
. It states that for positive real numbers a, b and c we have:
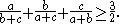
First proof
Starting from Nesbitt's inequality(1903)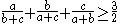we transform the left hand side:
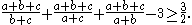
Now this can be transformed into:
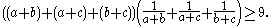
Division by 3 and the right factor yields:
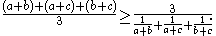
Now on the left we have the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
and on the right the harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
, so this inequality is true.
We might also want to try to use GM for three variables.
Second proof
Suppose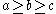, we have that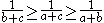define
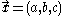
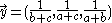
The scalar product of the two sequences is maximum because of the Rearrangement inequality if they are arranged the same way, call
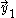and 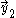the vector 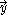shifted by one and by two, we have: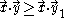Addition yields Nesbitt's inequality.
Third proof
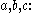
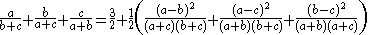
The following identity is true for allThis clearly proves that the left side is no less than
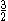for positive a,b and c.Note: every rational inequality can be solved by transforming it to the appropriate identity, see Hilbert's seventeenth problem
Hilbert's seventeenth problem
Hilbert's seventeenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It entails expression of definite rational functions as quotients of sums of squares...
.
Fourth proof
Starting from Nesbitt's inequality(1903)We add
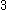to both sides.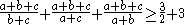Now this can be transformed into:
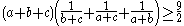
Multiply by
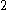on both sides.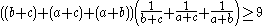Which is true by the Cauchy-Schwarz inequality.
Fifth proof
Starting from Nesbitt's inequality (1903)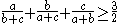,we substitute a+b=x, b+c=y, c+a=z.
Now, we get
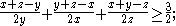
this can be transformed to
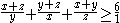
which is true, by inequality of arithmetic and geometric means
Inequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
.
Note
External links
- See mathlinks for more proofs of this inequality.