
Shapiro inequality
Encyclopedia
In mathematics
, the Shapiro inequality is an inequality proposed by H. Shapiro in 1954.
and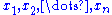 are positive numbers and:
are positive numbers and:
Then the Shapiro inequality states that
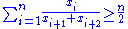
where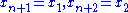 .
.
For greater values of n the inequality does not hold and the strict lower bound is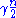 with
with 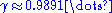 .
.
The initial proofs of the inequality in the pivotal cases n = 12 (Godunova and Levin, 1976) and n = 23 (Troesch, 1989) rely on numerical computations. In 2002, P.J. Bushell and J.B. McLeod published an analytical proof for n = 12.
The value of γ was determined in 1971 by Vladimir Drinfel'd
, who won a Fields Medal
in 1990. Specifically, Drinfel'd showed that the strict lower bound γ is given by , where ψ is the function convex hull of f(x) = e−x and
, where ψ is the function convex hull of f(x) = e−x and  . (That is, the region above the graph of ψ is the convex hull
. (That is, the region above the graph of ψ is the convex hull
of the union of the regions above the graphs of f and g.)
Interior local mimima of the left-hand side are always ≥ n/2 (Nowosad, 1968).
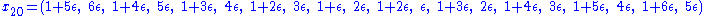 where
where  is close to 0.
is close to 0.
Then the left-hand side is equal to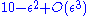 , thus lower than 10 when
, thus lower than 10 when  is small enough.
is small enough.
The following counter-example for n = 14 is by Troesch (1985):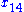 = (0, 42, 2, 42, 4, 41, 5, 39, 4, 38, 2, 38, 0, 40) (Troesch, 1985)
= (0, 42, 2, 42, 4, 41, 5, 39, 4, 38, 2, 38, 0, 40) (Troesch, 1985)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Shapiro inequality is an inequality proposed by H. Shapiro in 1954.
Statement of the inequality
Suppose n is a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
and
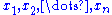 are positive numbers and:
are positive numbers and:- n is even and less than or equal to 12, or
- n is odd and less than or equal to 23.
Then the Shapiro inequality states that
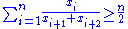
where
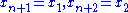 .
.For greater values of n the inequality does not hold and the strict lower bound is
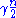 with
with 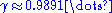 .
.The initial proofs of the inequality in the pivotal cases n = 12 (Godunova and Levin, 1976) and n = 23 (Troesch, 1989) rely on numerical computations. In 2002, P.J. Bushell and J.B. McLeod published an analytical proof for n = 12.
The value of γ was determined in 1971 by Vladimir Drinfel'd
Vladimir Drinfel'd
Vladimir Gershonovich Drinfel'd is a Ukrainian and Soviet mathematician at the University of Chicago.The work of Drinfeld related algebraic geometry over finite fields with number theory, especially the theory of automorphic forms, through the notions of elliptic module and the theory of the...
, who won a Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
in 1990. Specifically, Drinfel'd showed that the strict lower bound γ is given by
 , where ψ is the function convex hull of f(x) = e−x and
, where ψ is the function convex hull of f(x) = e−x and  . (That is, the region above the graph of ψ is the convex hull
. (That is, the region above the graph of ψ is the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the union of the regions above the graphs of f and g.)
Interior local mimima of the left-hand side are always ≥ n/2 (Nowosad, 1968).
Counter-examples for higher n
The first counter-example was found by Lighthill in 1956, for n = 20: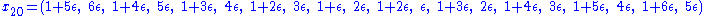 where
where  is close to 0.
is close to 0.Then the left-hand side is equal to
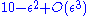 , thus lower than 10 when
, thus lower than 10 when  is small enough.
is small enough.The following counter-example for n = 14 is by Troesch (1985):
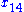 = (0, 42, 2, 42, 4, 41, 5, 39, 4, 38, 2, 38, 0, 40) (Troesch, 1985)
= (0, 42, 2, 42, 4, 41, 5, 39, 4, 38, 2, 38, 0, 40) (Troesch, 1985)External links
- Shapiro's Cyclic Inequality for Even n, P.J. Bushell and J.B. McLeod, J. of Inequal. & Appl., 2002, Vol. 7(3), pp. 331–349. They give an analytic proof of the formula for even n ≤ 12, from which the result for all n ≤ 12 follows. They state n = 23 as an open problem.
- Usenet discussion in 1999 (Dave Rusin's notes)
- PlanetMath

