Nested intervals
Encyclopedia
In mathematics
, a sequence of nested intervals is understood as a collection of sets of real numbers
such that each set In is an interval of the real line, for n = 1, 2, 3, ... , and that further
for all n. In other words, the intervals diminish, with the left-hand end moving only towards the right, and the right-hand end only to the left.
The main question to be posed is the nature of the intersection
of all the In. Without any further information, all that can be said is that the intersection J of all the In, i.e. the set of all points common to the intervals, is either the empty set
, a point, or some interval.
The possibility of an empty intersection can be illustrated by the intersection when In is the open interval.
Here the intersection is empty, because no number x is both > 0 and less than every fraction 2−n.
The situation is different for closed intervals. The nested intervals theorem states that if each In is a closed and bounded interval, say
with
then under the assumption of nesting, the intersection of the In is not empty. It may be a singleton set {c}, or another closed interval [a, b]. More explicitly, the requirement of nesting means that
and
One can consider the complement of each interval, written as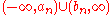
. By De Morgan's laws, the complement of the intersection is a union of two disjoint open sets. By the connectedness
of the real line
there must be something between them. This shows that the intersection of (even an uncountable number of) nested, closed, and bounded intervals is nonempty.
to classify the singular behaviour of certain differential equation
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a sequence of nested intervals is understood as a collection of sets of real numbers
- In
such that each set In is an interval of the real line, for n = 1, 2, 3, ... , and that further
- In + 1 is a subset of In
for all n. In other words, the intervals diminish, with the left-hand end moving only towards the right, and the right-hand end only to the left.
The main question to be posed is the nature of the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of all the In. Without any further information, all that can be said is that the intersection J of all the In, i.e. the set of all points common to the intervals, is either the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, a point, or some interval.
The possibility of an empty intersection can be illustrated by the intersection when In is the open interval.
Here the intersection is empty, because no number x is both > 0 and less than every fraction 2−n.
The situation is different for closed intervals. The nested intervals theorem states that if each In is a closed and bounded interval, say
- In = [an, bn]
with
- an ≤ bn
then under the assumption of nesting, the intersection of the In is not empty. It may be a singleton set {c}, or another closed interval [a, b]. More explicitly, the requirement of nesting means that
- an ≤ an + 1
and
- bn ≥ bn + 1.
One can consider the complement of each interval, written as
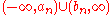. By De Morgan's laws, the complement of the intersection is a union of two disjoint open sets. By the connectednessConnectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
there must be something between them. This shows that the intersection of (even an uncountable number of) nested, closed, and bounded intervals is nonempty.
Higher dimensions
In two dimensions there is a similar result: nested closed disks in the plane must have a common intersection. This result was shown by Hermann WeylHermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
to classify the singular behaviour of certain differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s.