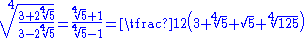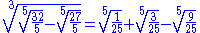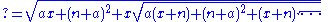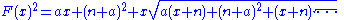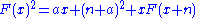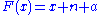Nested radicals
Encyclopedia
In algebra
, a nested radical is a radical expression that contains another radical expression. Examples include:
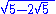
which arises in discussing the regular pentagon
;
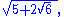
or more complicated ones such as:
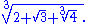
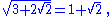
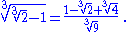
Rewriting a nested radical in this way is called denesting. This process is generally considered a difficult problem, although a special class of nested radical can be denested by assuming it denests into a sum of two surds:
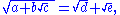
Squaring both sides:
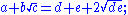
This can be solved by using the quadratic formula and setting rational and irrational parts on both sides of the equation equal to each other. The solutions for e and d are:
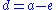
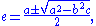
The solution d is the algebraic conjugate of e. If
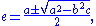
then
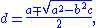
However, this approach works for nested radicals of the form

if and only if
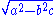
is an integer
, in which case the nested radical can be denested into a sum of surds.
In some cases, higher-power radicals may be needed to denest the nested radical.
introduced the first algorithm
for deciding which nested radicals can be denested. Earlier algorithms worked in some cases but not others.
demonstrated a number of curious identities involving denesting of radicals. Among them are the following:
Ramanujan posed this problem to the 'Journal of Indian Mathematical Society':
This can be solved by noting a more general formulation:
Setting this to F(x) and squaring both sides gives us:
Which can be simplified to:
It can then be shown that:
So, setting a =0, n = 1, and x = 2:
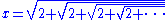
represent rational numbers. This rational number can be found by realizing that x also appears under the radical sign, which gives the equation
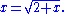
If we solve this equation, we find that x = 2 (the second solution x = −1 doesn't apply, under the convention that the positive square root is meant). This approach can also be used to show that generally, if n > 0, then:
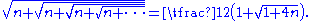
The same procedure also works to get
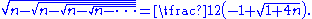
This method will give a rational x value for all values of n such that
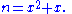
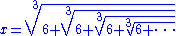
can represent rational numbers as well. Again, by realizing that the whole expression appears inside itself, we are left with the equation
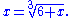
If we solve this equation, we find that x = 2. More generally, we find that
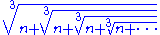
is the real root of the equation x3 − x − n = 0 for all n > 0.
The same procedure also works to get
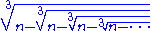
as the real root of the equation x3 + x − n = 0 for all n and x where n > 0 and |x| ≥ 1. This root is the plastic number
ρ, approximately equal to 1.3247.
(Contributed by RSC)
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, a nested radical is a radical expression that contains another radical expression. Examples include:
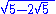
which arises in discussing the regular pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
;
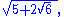
or more complicated ones such as:
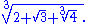
Denesting nested radicals
Some nested radicals can be rewritten in a form that is not nested. For example,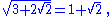
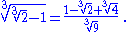
Rewriting a nested radical in this way is called denesting. This process is generally considered a difficult problem, although a special class of nested radical can be denested by assuming it denests into a sum of two surds:
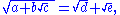
Squaring both sides:
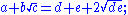
This can be solved by using the quadratic formula and setting rational and irrational parts on both sides of the equation equal to each other. The solutions for e and d are:
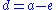
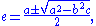
The solution d is the algebraic conjugate of e. If
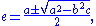
then
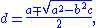
However, this approach works for nested radicals of the form

if and only if
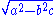
is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, in which case the nested radical can be denested into a sum of surds.
In some cases, higher-power radicals may be needed to denest the nested radical.
Landau's algorithm
In 1989 Susan LandauSusan Landau
Susan Landau is an American mathematician and engineer, as of 2011, a Visiting Scholar at the Computer Science Department, Harvard University....
introduced the first algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for deciding which nested radicals can be denested. Earlier algorithms worked in some cases but not others.
Some identities of Ramanujan
Srinivasa RamanujanSrinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
demonstrated a number of curious identities involving denesting of radicals. Among them are the following:
Ramanujan posed this problem to the 'Journal of Indian Mathematical Society':
This can be solved by noting a more general formulation:
Setting this to F(x) and squaring both sides gives us:
Which can be simplified to:
It can then be shown that:
So, setting a =0, n = 1, and x = 2:
-
 (Contributed by RSC)
(Contributed by RSC)
Square roots
Under certain conditions infinitely nested square roots such as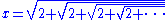
represent rational numbers. This rational number can be found by realizing that x also appears under the radical sign, which gives the equation
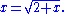
If we solve this equation, we find that x = 2 (the second solution x = −1 doesn't apply, under the convention that the positive square root is meant). This approach can also be used to show that generally, if n > 0, then:
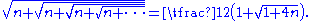
The same procedure also works to get
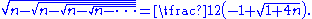
This method will give a rational x value for all values of n such that
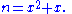
Cube roots
In certain cases, infinitely nested cube roots such as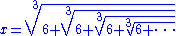
can represent rational numbers as well. Again, by realizing that the whole expression appears inside itself, we are left with the equation
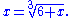
If we solve this equation, we find that x = 2. More generally, we find that
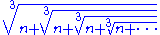
is the real root of the equation x3 − x − n = 0 for all n > 0.
The same procedure also works to get
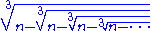
as the real root of the equation x3 + x − n = 0 for all n and x where n > 0 and |x| ≥ 1. This root is the plastic number
Plastic number
In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, ....
ρ, approximately equal to 1.3247.
(Contributed by RSC)