The neusis is a geometric construction method that was used in antiquity by Greek mathematicians.

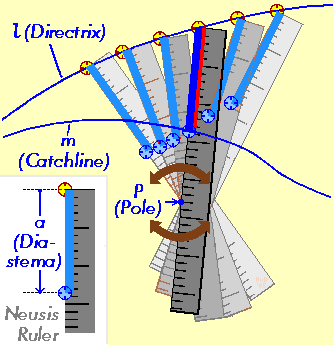
Geometric construction

The neusis construction (from Greek νεῦσις from νεύειν neuein "incline towards"; plural: νεύσεις neuseis) consists of fitting a line element of given length (a) in between two given lines (l and m), in such a way that the line element, or its extension, passes through a given point P. That is, one end of the line element has to lie on l, the other end on m, while the line element is "inclined" towards P.

A neusis construction might be performed by means of a 'Neusis Ruler': a marked ruler that is rotatable around the point P (this may be done by putting a pin into the point P and then pressing the ruler against the pin). In the figure one end of the ruler is marked with a yellow eye with crosshairs: this is the origin of the scale division on the ruler. A second marking on the ruler (the blue eye) indicates the distance a from the origin. The yellow eye is moved along line l, until the blue eye coincides with line m. The position of the line element thus found is shown in the figure as a dark blue bar.

Point P is called the pole of the neusis, line l the directrix, or guiding line, and line m the catch line. Length a is called the diastema (διάστημα; Greek for "distance").

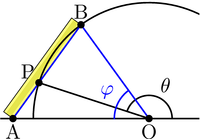
Use of the neusis

Neuseis have been important because they sometimes provide a means to solve geometric problems that are not solvable by means of compass and straightedge

Compass and straightedge

Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....

 alone. Examples are the trisection of any angle in three equal parts, or the construction

Constructible polygon

In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....

 of a regular heptagon. Mathematicians such as Archimedes

Archimedes

Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...

 of Syracuse (287–212 BC) freely used neuseis. Nevertheless, gradually the technique dropped out of use.

Waning popularity

T. L. Heath

T. L. Heath

Sir Thomas Little Heath was a British civil servant, mathematician, classical scholar, historian of ancient Greek mathematics, translator, and mountaineer. He was educated at Clifton College...

, the historian of mathematics, has suggested that the Greek mathematician Oenopides

Oenopides

Oenopides of Chios was an ancient Greek mathematician and astronomer, who lived around 450 BCE. He was born shortly after 500 BCE on the island of Chios, but mostly worked in Athens.- Astronomy :...

 (ca. 440 BC) was the first to put compass and straightedge constructions above neuseis. The principle to avoid neuseis whenever possible, may have been spread by Hippocrates of Chios

Hippocrates of Chios

Hippocrates of Chios was an ancient Greek mathematician, , and astronomer, who lived c. 470 – c. 410 BCE.He was born on the isle of Chios, where he originally was a merchant. After some misadventures he went to Athens, possibly for litigation...

 (ca. 430 BC), who originated from the same island as Oenopides, and who was—as far as we know—the first to write a systematically ordered geometry textbook. One hundred years after him Euclid

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

 too shunned neuseis in his very influential textbook, The Elements.

The next attack on the neusis came when, from the fourth century BC, Plato

Plato

Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...

's idealism

Idealism

In philosophy, idealism is the family of views which assert that reality, or reality as we can know it, is fundamentally mental, mentally constructed, or otherwise immaterial. Epistemologically, idealism manifests as a skepticism about the possibility of knowing any mind-independent thing...

 gained ground. Under its influence a hierarchy of three classes of geometrical constructions was developed. Descending from the "abstract and noble" to the "mechanical and earthly", the three classes were:

1. constructions with straight lines and circles only (compass and straightedge);
2. constructions that in addition to this use conic sections (ellipse
   Ellipse
   In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
   
   s, parabola
   Parabola
   In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
   
   s, hyperbola
   Hyperbola
   In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
   
   s);
3. constructions that needed yet other means of construction, for example neuseis.

In the end the use of neusis was deemed acceptable only when the two other, higher categories of constructions did not offer a solution. Neusis became a kind of last resort that was invoked only when all other, more respectable, methods had failed. Using neusis where other construction methods might have been used, was branded by the late Greek mathematician Pappus of Alexandria

Pappus of Alexandria

Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...

(ca. 325 AD) as "a not inconsiderable error".

External links

• MathWorld page
• Angle Trisection by Paper Folding