
Newton–Pepys problem
Encyclopedia
The Newton–Pepys problem is a probability
problem concerning the probability of throwing sixes from a certain number of dice.
In 1693 Samuel Pepys
and Isaac Newton
corresponded over a problem posed by Pepys in relation to a wager
he planned to make. The problem was:
Pepys initially thought that outcome C had the highest probability, but Newton correctly concluded that outcome A actually has the highest probability.
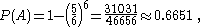
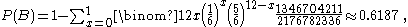
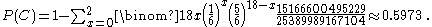
These results may be obtained by applying the binomial distribution (although Newton obtained them from first principles). In general, if P(N) is the probability of throwing at least n sixes with 6n dice, then:
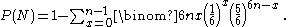
As n grows, P(N) decreases monotonically towards an asymptotic limit of 1/2.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
problem concerning the probability of throwing sixes from a certain number of dice.
In 1693 Samuel Pepys
Samuel Pepys
Samuel Pepys FRS, MP, JP, was an English naval administrator and Member of Parliament who is now most famous for the diary he kept for a decade while still a relatively young man...
and Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
corresponded over a problem posed by Pepys in relation to a wager
Gambling
Gambling is the wagering of money or something of material value on an event with an uncertain outcome with the primary intent of winning additional money and/or material goods...
he planned to make. The problem was:
- Which of the following three propositions has the greatest chance of success?
-
- A. Six fair dice are tossed independently and at least one “6” appears.
- B. Twelve fair dice are tossed independently and at least two “6”s appear.
- C. Eighteen fair dice are tossed independently and at least three “6”s appear.
Pepys initially thought that outcome C had the highest probability, but Newton correctly concluded that outcome A actually has the highest probability.
Solution
The probabilities of outcomes A, B and C are: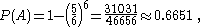
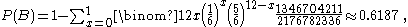
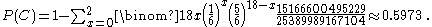
These results may be obtained by applying the binomial distribution (although Newton obtained them from first principles). In general, if P(N) is the probability of throwing at least n sixes with 6n dice, then:
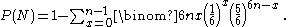
As n grows, P(N) decreases monotonically towards an asymptotic limit of 1/2.

