
Nielsen theory
Encyclopedia
Nielsen theory is a branch of mathematical research with its origins in topological fixed point theory. Its central ideas were developed by Danish mathematician Jakob Nielsen
, and bear his name.
The theory developed in the study of the so-called minimal number of a map
f from a compact space to itself, denoted MF[f]. This is defined as: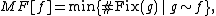
where ~ indicates homotopy
of mappings, and #Fix(g) indicates the number of fixed points of g. The minimal number was very difficult to compute in Nielsen's time, and remains so today. Nielsen's approach is to group the fixed point set into classes, which are judged "essential" or "nonessential" according to whether or not they can be "removed" by a homotopy.
Nielsen's original formulation is equivalent to the following:
We define an equivalence relation
on the set of fixed points of a self-map f on a space X. We say that x is equivalent to y if and only if there exists a path
c from x to y with f(c) homotopic to c as paths. The equivalence classes with respect to this relation are called the Nielsen classes of f, and the Nielsen number N(f) is defined as the number of Nielsen classes having non-zero fixed point index
sum.
Nielsen proved that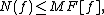
making his invariant a good tool for estimating the much more difficult MF[f]. This leads immediately to what is now known as the Nielsen fixed point theorem: Any map f has at least N(f) fixed points.
Because of its definition in terms of the fixed point index
, the Nielsen number is closely related to the Lefschetz number. Indeed, shortly after Nielsen's initial work, the two invariants were combined into a single "generalized Lefschetz number" (more recently called the Reidemeister trace) by Wecken and Reidemeister.
Jakob Nielsen (mathematician)
Jakob Nielsen was a Danish mathematician known for his work on automorphisms of surfaces. He was born in the village Mjels on the island of Als in North Schleswig, in modern day Denmark. His mother died when he was 3, and in 1900 he went to live with his aunt and was enrolled in the Realgymnasium...
, and bear his name.
The theory developed in the study of the so-called minimal number of a map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
f from a compact space to itself, denoted MF[f]. This is defined as:
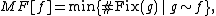
where ~ indicates homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
of mappings, and #Fix(g) indicates the number of fixed points of g. The minimal number was very difficult to compute in Nielsen's time, and remains so today. Nielsen's approach is to group the fixed point set into classes, which are judged "essential" or "nonessential" according to whether or not they can be "removed" by a homotopy.
Nielsen's original formulation is equivalent to the following:
We define an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the set of fixed points of a self-map f on a space X. We say that x is equivalent to y if and only if there exists a path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
c from x to y with f(c) homotopic to c as paths. The equivalence classes with respect to this relation are called the Nielsen classes of f, and the Nielsen number N(f) is defined as the number of Nielsen classes having non-zero fixed point index
Fixed point index
In mathematics, the fixed-point index is a concept in topological fixed-point theory, and in particular Nielsen theory. The fixed-point index can be thought of as a multiplicity measurement for fixed points....
sum.
Nielsen proved that
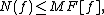
making his invariant a good tool for estimating the much more difficult MF[f]. This leads immediately to what is now known as the Nielsen fixed point theorem: Any map f has at least N(f) fixed points.
Because of its definition in terms of the fixed point index
Fixed point index
In mathematics, the fixed-point index is a concept in topological fixed-point theory, and in particular Nielsen theory. The fixed-point index can be thought of as a multiplicity measurement for fixed points....
, the Nielsen number is closely related to the Lefschetz number. Indeed, shortly after Nielsen's initial work, the two invariants were combined into a single "generalized Lefschetz number" (more recently called the Reidemeister trace) by Wecken and Reidemeister.
External links
- Survey article on Nielsen theory by Robert F. Brown at Topology Atlas

