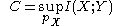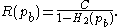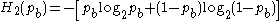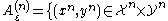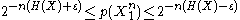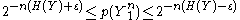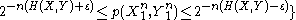Noisy channel coding theorem
Encyclopedia
In information theory
, the noisy-channel coding theorem (sometimes Shannon's theorem), establishes that for any given degree of noise
contamination of a communication channel, it is possible to communicate discrete data (digital information
) nearly error-free up to a computable maximum rate through the channel. This result was presented by Claude Shannon in 1948 and was based in part on earlier work and ideas of Harry Nyquist
and Ralph Hartley
.
The Shannon limit or Shannon capacity of a communications channel is the theoretical maximum information transfer rate
of the channel, for a particular noise level.
. This theorem is of foundational importance to the modern field of information theory
. Shannon only gave an outline of the proof. The first rigorous proof is due to Amiel Feinstein in 1954.
The Shannon theorem states that given a noisy channel with channel capacity
C and information transmitted at a rate R, then if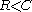 there exist code
there exist code
s that allow the probability of error
at the receiver to be made arbitrarily small. This means that, theoretically, it is possible to transmit information nearly without error at any rate below a limiting rate, C.
The converse is also important. If , an arbitrarily small probability of error is not achievable. All codes will have a probability of error greater than a certain positive minimal level, and this level increases as the rate increases. So, information cannot be guaranteed to be transmitted reliably across a channel at rates beyond the channel capacity. The theorem does not address the rare situation in which rate and capacity are equal.
, an arbitrarily small probability of error is not achievable. All codes will have a probability of error greater than a certain positive minimal level, and this level increases as the rate increases. So, information cannot be guaranteed to be transmitted reliably across a channel at rates beyond the channel capacity. The theorem does not address the rare situation in which rate and capacity are equal.
The channel capacity C can be calculated from the physical properties of a channel; for a band-limited channel with Gaussian noise, using the Shannon–Hartley theorem
.
Simple schemes such as "send the message 3 times and use a best 2 out of 3 voting scheme if the copies differ" are inefficient error-correction methods, unable to asymptotically guarantee that a block of data can be communicated free of error. Advanced techniques such as Reed–Solomon codes and, more recently, turbo code
s come much closer to reaching the theoretical Shannon limit, but at a cost of high computational complexity. Using low-density parity-check
(LDPC) codes or turbo codes and with the computing power in today's digital signal processors, it is now possible to reach very close to the Shannon limit. In fact, it was shown that LDPC codes can reach within 0.0045 dB of the Shannon limit (for very long block lengths).
 Theorem (Shannon, 1948):
Theorem (Shannon, 1948):
(MacKay (2003), p. 162; cf Gallager (1968), ch.5; Cover and Thomas (1991), p. 198; Shannon (1948) thm. 11)
The following outlines are only one set of many different styles available for study in information theory texts.
(AEP). Another style can be found in information theory texts using error exponent
s.
Both types of proofs make use of a random coding argument where the codebook used across a channel is randomly constructed - this serves to reduce computational complexity while still proving the existence of a code satisfying a desired low probability of error at any data rate below the channel capacity
.
By an AEP-related argument, given a channel, length strings of source symbols
strings of source symbols 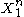 , and length
, and length  strings of channel outputs
strings of channel outputs 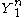 , we can define a jointly typical set by the following:
, we can define a jointly typical set by the following:
We say that two sequences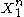 và
và 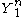 are jointly typical if they lie in the jointly typical set defined above.
are jointly typical if they lie in the jointly typical set defined above.
Steps
The probability of error of this scheme is divided into two parts:
Define: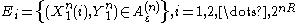
as the event that message i is jointly typical with the sequence received when message 1 is sent.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, the noisy-channel coding theorem (sometimes Shannon's theorem), establishes that for any given degree of noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
contamination of a communication channel, it is possible to communicate discrete data (digital information
Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
) nearly error-free up to a computable maximum rate through the channel. This result was presented by Claude Shannon in 1948 and was based in part on earlier work and ideas of Harry Nyquist
Harry Nyquist
Harry Nyquist was an important contributor to information theory.-Personal life:...
and Ralph Hartley
Ralph Hartley
Ralph Vinton Lyon Hartley was an electronics researcher. He invented the Hartley oscillator and the Hartley transform, and contributed to the foundations of information theory.-Biography:...
.
The Shannon limit or Shannon capacity of a communications channel is the theoretical maximum information transfer rate
Code rate
In telecommunication and information theory, the code rate of a forward error correction code is the proportion of the data-stream that is useful...
of the channel, for a particular noise level.
Overview
Stated by Claude Shannon in 1948, the theorem describes the maximum possible efficiency of error-correcting methods versus levels of noise interference and data corruption. The theory doesn't describe how to construct the error-correcting method, it only tells us how good the best possible method can be. Shannon's theorem has wide-ranging applications in both communications and data storageData storage device
thumb|200px|right|A reel-to-reel tape recorder .The magnetic tape is a data storage medium. The recorder is data storage equipment using a portable medium to store the data....
. This theorem is of foundational importance to the modern field of information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. Shannon only gave an outline of the proof. The first rigorous proof is due to Amiel Feinstein in 1954.
The Shannon theorem states that given a noisy channel with channel capacity
Channel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
C and information transmitted at a rate R, then if
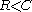 there exist code
there exist codeCode
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
s that allow the probability of error
Probability of error
In statistics, the term "error" arises in two ways. Firstly, it arises in the context of decision making, where the probability of error may be considered as being the probability of making a wrong decision and which would have a different value for each type of error...
at the receiver to be made arbitrarily small. This means that, theoretically, it is possible to transmit information nearly without error at any rate below a limiting rate, C.
The converse is also important. If
 , an arbitrarily small probability of error is not achievable. All codes will have a probability of error greater than a certain positive minimal level, and this level increases as the rate increases. So, information cannot be guaranteed to be transmitted reliably across a channel at rates beyond the channel capacity. The theorem does not address the rare situation in which rate and capacity are equal.
, an arbitrarily small probability of error is not achievable. All codes will have a probability of error greater than a certain positive minimal level, and this level increases as the rate increases. So, information cannot be guaranteed to be transmitted reliably across a channel at rates beyond the channel capacity. The theorem does not address the rare situation in which rate and capacity are equal.The channel capacity C can be calculated from the physical properties of a channel; for a band-limited channel with Gaussian noise, using the Shannon–Hartley theorem
Shannon–Hartley theorem
In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy channel coding theorem to the archetypal case of a continuous-time...
.
Simple schemes such as "send the message 3 times and use a best 2 out of 3 voting scheme if the copies differ" are inefficient error-correction methods, unable to asymptotically guarantee that a block of data can be communicated free of error. Advanced techniques such as Reed–Solomon codes and, more recently, turbo code
Turbo code
In information theory, turbo codes are a class of high-performance forward error correction codes developed in 1993, which were the first practical codes to closely approach the channel capacity, a theoretical maximum for the code rate at which reliable communication is still possible given a...
s come much closer to reaching the theoretical Shannon limit, but at a cost of high computational complexity. Using low-density parity-check
Low-density parity-check code
In information theory, a low-density parity-check code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel, and is constructed using a sparse bipartite graph...
(LDPC) codes or turbo codes and with the computing power in today's digital signal processors, it is now possible to reach very close to the Shannon limit. In fact, it was shown that LDPC codes can reach within 0.0045 dB of the Shannon limit (for very long block lengths).
Mathematical statement

- 1. For every discrete memoryless channel, the channel capacityChannel capacityIn electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
- has the following property. For any ε > 0 and R < C, for large enough N, there exists a code of length N and rate ≥ R and a decoding algorithm, such that the maximal probability of block error is ≤ ε.
- 2. If a probability of bit error pb is acceptable, rates up to R(pb) are achievable, where
- and
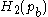 is the binary entropy function
is the binary entropy function
- 3. For any pb, rates greater than R(pb) are not achievable.
(MacKay (2003), p. 162; cf Gallager (1968), ch.5; Cover and Thomas (1991), p. 198; Shannon (1948) thm. 11)
Outline of proof
As with several other major results in information theory, the proof of the noisy channel coding theorem includes an achievability result and a matching converse result. These two components serve to bound, in this case, the set of possible rates at which one can communicate over a noisy channel, and matching serves to show that these bounds are tight bounds.The following outlines are only one set of many different styles available for study in information theory texts.
Achievability for discrete memoryless channels
This particular proof of achievability follows the style of proofs that make use of the asymptotic equipartition propertyAsymptotic equipartition property
In information theory the asymptotic equipartition property is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of compression....
(AEP). Another style can be found in information theory texts using error exponent
Error exponent
In information theory, the error exponent of a channel code or source code over the block length of the code is the logarithm of the error probability. For example, if the probability of error of a decoder drops as e–nα, where n is the block length, the error exponent is α...
s.
Both types of proofs make use of a random coding argument where the codebook used across a channel is randomly constructed - this serves to reduce computational complexity while still proving the existence of a code satisfying a desired low probability of error at any data rate below the channel capacity
Channel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
.
By an AEP-related argument, given a channel, length
 strings of source symbols
strings of source symbols 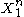 , and length
, and length  strings of channel outputs
strings of channel outputs 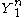 , we can define a jointly typical set by the following:
, we can define a jointly typical set by the following:We say that two sequences
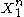 và
và 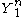 are jointly typical if they lie in the jointly typical set defined above.
are jointly typical if they lie in the jointly typical set defined above.Steps
- In the style of the random coding argument, we randomly generate
 codewords of length n from a probability distribution Q.
codewords of length n from a probability distribution Q. - This code is revealed to the sender and receiver. It is also assumed that one knows the transition matrix
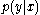 for the channel being used.
for the channel being used. - A message W is chosen according to the uniform distribution on the set of codewords. That is,
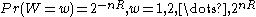 .
. - The message W is sent across the channel.
- The receiver receives a sequence according to
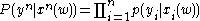
- Sending these codewords across the channel, we receive
 , and decode to some source sequence if there exists exactly 1 codeword that is jointly typical with Y. If there are no jointly typical codewords, or if there are more than one, an error is declared. An error also occurs if a decoded codeword doesn't match the original codeword. This is called typical set decoding.
, and decode to some source sequence if there exists exactly 1 codeword that is jointly typical with Y. If there are no jointly typical codewords, or if there are more than one, an error is declared. An error also occurs if a decoded codeword doesn't match the original codeword. This is called typical set decoding.
The probability of error of this scheme is divided into two parts:
- First, error can occur if no jointly typical X sequences are found for a received Y sequence
- Second, error can occur if an incorrect X sequence is jointly typical with a received Y sequence.
- By the randomness of the code construction, we can assume that the average probability of error averaged over all codes does not depend on the index sent. Thus, without loss of generality, we can assume W = 1.
- From the joint AEP, we know that the probability that no jointly typical X exists goes to 0 as n grows large. We can bound this error probability by
 .
.
- Also from the joint AEP, we know the probability that a particular
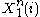 and the
and the 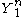 resulting from W = 1 are jointly typical is
resulting from W = 1 are jointly typical is 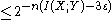 .
.
Define:
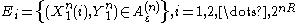
as the event that message i is jointly typical with the sequence received when message 1 is sent.
-
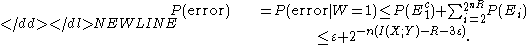
We can observe that as goes to infinity, if
goes to infinity, if  for the channel, the probability of error will go to 0.
for the channel, the probability of error will go to 0.
Finally, given that the average codebook is shown to be "good," we know that there exists a codebook whose performance is better than the average, and so satisfies our need for arbitrarily low error probability communicating across the noisy channel.
Weak converse for discrete memoryless channels
Suppose a code of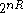 codewords. Let W be drawn uniformly over this set as an index. Let
codewords. Let W be drawn uniformly over this set as an index. Let 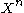 and
and  be the codewords and received codewords, respectively.
be the codewords and received codewords, respectively.
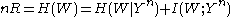 using identities involving entropy and mutual information
using identities involving entropy and mutual information since X is a function of W
since X is a function of W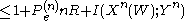 by the use of Fano's InequalityFano's inequalityIn information theory, Fano's inequality relates the average information lost in a noisy channel to the probability of the categorization error. It was derived by Robert Fano in the early 1950s while teaching a Ph.D...
by the use of Fano's InequalityFano's inequalityIn information theory, Fano's inequality relates the average information lost in a noisy channel to the probability of the categorization error. It was derived by Robert Fano in the early 1950s while teaching a Ph.D... by the fact that capacity is maximized mutual information.
by the fact that capacity is maximized mutual information.
The result of these steps is that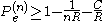 . As the block length
. As the block length  goes to infinity, we obtain
goes to infinity, we obtain 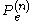 is bounded away from 0 if R is greater than C - we can get arbitrarily low rates of error only if R is less than C.
is bounded away from 0 if R is greater than C - we can get arbitrarily low rates of error only if R is less than C.
Strong converse for discrete memoryless channels
A strong converse theorem, proven by Wolfowitz in 1957, states that,
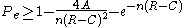
for some finite positive constant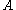 . While the weak converse states that the error probability is bounded away from zero as
. While the weak converse states that the error probability is bounded away from zero as  goes to infinity, the strong converse states that the error goes exponentially to 1. Thus,
goes to infinity, the strong converse states that the error goes exponentially to 1. Thus, 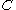 is a sharp threshold between perfectly reliable and completely unreliable communication.
is a sharp threshold between perfectly reliable and completely unreliable communication.
Channel coding theorem for non-stationary memoryless channels
We assume that the channel is memoryless, but its transition probabilities change with time, in a fashion known at the transmitter as well as the receiver.
Then the channel capacity is given by
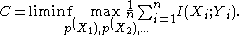
The maximum is attained at the capacity achieving distributions for each respective channel. That is,
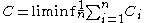
where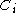 is the capacity of the ith channel.
is the capacity of the ith channel.
Outline of the proof
The proof runs through in almost the same way as that of channel coding theorem. Achievability follows from random coding with each symbol chosen randomly from the capacity achieving distribution for that particular channel. Typicality arguments use the definition of typical sets for non-stationary sources defined in the asymptotic equipartition propertyAsymptotic equipartition propertyIn information theory the asymptotic equipartition property is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of compression....
article.
The technicality of lim inf comes into play when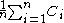 does not converge.
does not converge.
See also
- Asymptotic equipartition propertyAsymptotic equipartition propertyIn information theory the asymptotic equipartition property is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of compression....
(AEP) - Turbo codeTurbo codeIn information theory, turbo codes are a class of high-performance forward error correction codes developed in 1993, which were the first practical codes to closely approach the channel capacity, a theoretical maximum for the code rate at which reliable communication is still possible given a...
- Fano's InequalityFano's inequalityIn information theory, Fano's inequality relates the average information lost in a noisy channel to the probability of the categorization error. It was derived by Robert Fano in the early 1950s while teaching a Ph.D...
- Shannon's source coding theorem
- Shannon–Hartley theoremShannon–Hartley theoremIn information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy channel coding theorem to the archetypal case of a continuous-time...
- Rate-distortion theory
External links
- On Shannon and Shannon's law
- Shannon's Noisy Channel Coding Theorem
- On-line textbook: Information Theory, Inference, and Learning Algorithms, by David MacKayDavid MacKay (scientist)David John Cameron MacKay, FRS, is the professor of natural philosophy in the department of Physics at the University of Cambridge and chief scientific adviser to the UK Department of Energy and Climate Change...
- gives an entertaining and thorough introduction to Shannon theory, including two proofs of the noisy-channel coding theorem. This text also discusses state-of-the-art methods from coding theory, such as low-density parity-check codeLow-density parity-check codeIn information theory, a low-density parity-check code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel, and is constructed using a sparse bipartite graph...
s, and Turbo codeTurbo codeIn information theory, turbo codes are a class of high-performance forward error correction codes developed in 1993, which were the first practical codes to closely approach the channel capacity, a theoretical maximum for the code rate at which reliable communication is still possible given a...
s.