
Non-dictatorship
Encyclopedia
In voting theory, non-dictatorship is a property of social choice functions, where the results cannot simply mirror that of any ONE single person's preferences without consideration of the other voters. Fairness requires that the social welfare function take into account the desires of more than one voter. In other words, there is no one voter with P as his/her individual preference order, such that P is the societal ("winning") preference order, unless all voters have the same P. Thus, as long as there are voters in the society that have different preference orderings, the preferences of individual i should not always prevail.
Non-dictatorship: No voter in the society is a dictator in the sense that, there does not exist a single voter i in the society such that for every set of orderings in the domain and every pair of distinct social states x and y, if voter i strictly prefers x over y, x is socially selected over y.
Anonymous voting systems (with at least two voters) automatically satisfy the non-dictatorship property.
Non-dictatorship: No voter in the society is a dictator in the sense that, there does not exist a single voter i in the society such that for every set of orderings in the domain and every pair of distinct social states x and y, if voter i strictly prefers x over y, x is socially selected over y.
There is no voter i in {1, ..., n} such that for every set of orderings in the domain of the constitution and every pair of social states x and y, x 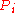 y implies x P y. y implies x P y. |
Anonymous voting systems (with at least two voters) automatically satisfy the non-dictatorship property.
See also
- Arrow's impossibility theoremArrow's impossibility theoremIn social choice theory, Arrow’s impossibility theorem, the General Possibility Theorem, or Arrow’s paradox, states that, when voters have three or more distinct alternatives , no voting system can convert the ranked preferences of individuals into a community-wide ranking while also meeting a...
(also known as Arrow's Paradox) - Social Choice and Individual ValuesSocial Choice and Individual ValuesKenneth Arrow's monograph Social Choice and Individual Values and a theorem within it created modern social choice theory, a rigorous melding of social ethics and voting theory with an economic flavor...

