Non-sinusoidal waveforms are waveform

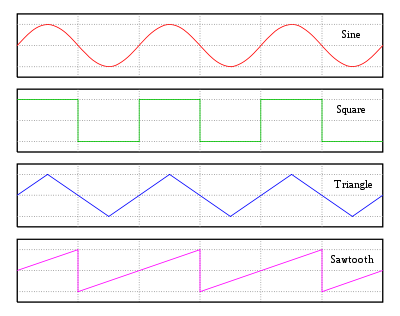
Waveform

Waveform means the shape and form of a signal such as a wave moving in a physical medium or an abstract representation.In many cases the medium in which the wave is being propagated does not permit a direct visual image of the form. In these cases, the term 'waveform' refers to the shape of a graph...

s that are not pure sine wave

Sine wave

The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...

s. They are usually derived from simple math functions. While a pure sine consists of a single frequency, non-sinusoidal waveforms can be described as containing multiple sine waves of different frequencies. These "component" sine waves may, or may not, be multiples of a fundamental

Fundamental frequency

The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...

 or "lowest" frequency. The frequency and amplitude of each component can be found using a mathematical technique known as Fourier analysis.

Non-sinusoidal waveforms are important in, for example, mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, music

Music

Music is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...

 and electronics

Electronics

Electronics is the branch of science, engineering and technology that deals with electrical circuits involving active electrical components such as vacuum tubes, transistors, diodes and integrated circuits, and associated passive interconnection technologies...

.

Examples of non-sinusoidal waveforms include square wave

Square wave

A square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...

s, rectangular wave

Pulse wave

A pulse wave or pulse train is a kind of non-sinusoidal waveform that is similar to a square wave, but does not have the symmetrical shape associated with a perfect square wave. It is a term common to synthesizer programming, and is a typical waveform available on many synths. The exact shape of...

s, ramp waves, triangle wave

Triangle wave

A triangle wave is a non-sinusoidal waveform named for its triangular shape.Like a square wave, the triangle wave contains only odd harmonics...

s, spiked waves, trapezoidal waves and sawtooth wave

Sawtooth wave

The sawtooth wave is a kind of non-sinusoidal waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw....

s.