Non-standard positional numeral systems
Encyclopedia
Non-standard positional numeral systems here designates numeral system
s that may be denoted positional systems
, but that deviate in one way or another from the following description of standard positional systems:
This article summarizes facts on some non-standard positional numeral systems. In most cases, the polynomial form in the description of standard systems still applies.
Certain historical numeral systems like the Babylonian (standard) sexagesimal notation or the Chinese
rod numerals could be classified as standard systems of base 60 and 10, respectively (unconventionally counting the space representing zero as a numeral). However, they could also be classified as non-standard systems (more specifically, mixed-base systems with unary components), if the primitive repeated glyph
s making up the numerals are considered.
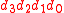given by the polynomial form can be simplified into 
since 
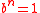for all n. Non-standard features of this system include:
is a particular system where the base is b=2. In the balanced ternary
system, the base is b=3, and the numerals have the values −1, 0 and +1 (rather than 0, 1 and 2 as in the standard ternary system
, or 1, 2 and 3 as in the bijective ternary system).
It can be generalized on other complex bases: Complex base systems
.
(phinary).
system such as the factorial number system, the weights form a sequence where each weight is an integral multiple of the previous one. Other sequences can be used, but then every integer may not have a unique representation. For example, Fibonacci coding
uses the digits 0 and 1, weighted according to the Fibonacci sequence (1, 2, 3, 5, 8, ...); a unique representation of all non-negative integers may be ensured by forbidding consecutive 1's.
For calendrical use, the Mayan
numeral system was a mixed radix system, since one of its positions represents a multiplication by 18 rather than 20, in order to fit a 360-day calendar. Also, giving an angle in degrees, minutes and seconds (with decimals), or a time in days, hours, minutes and seconds, can be interpreted as mixed radix systems.
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
s that may be denoted positional systems
Positional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
, but that deviate in one way or another from the following description of standard positional systems:
- In a standard positional numeral system, the base b is a positive integer, and b different numeralNumerical digitA digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
s are used to represent all non-negative integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Each numeral represents one of the values 0, 1, 2, etc., up to b-1, but the value also depends on the position of the digitNumerical digitA digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
in a number. The value of a digit string like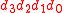
in base b is given by the polynomial form
-
.
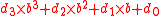- The numbers written in superscript represent the powersExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of the base used. - For instance, in hexadecimalHexadecimalIn mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
(b=16), using A=10, B=11 etc., the digit string 1F3A means
-
.
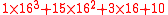- Introducing a radix pointRadix pointIn mathematics and computing, a radix point is the symbol used in numerical representations to separate the integer part of a number from its fractional part . "Radix point" is a general term that applies to all number bases...
"." and a minus sign "–", all real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s can be represented.
This article summarizes facts on some non-standard positional numeral systems. In most cases, the polynomial form in the description of standard systems still applies.
Certain historical numeral systems like the Babylonian (standard) sexagesimal notation or the Chinese
China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
rod numerals could be classified as standard systems of base 60 and 10, respectively (unconventionally counting the space representing zero as a numeral). However, they could also be classified as non-standard systems (more specifically, mixed-base systems with unary components), if the primitive repeated glyph
Glyph
A glyph is an element of writing: an individual mark on a written medium that contributes to the meaning of what is written. A glyph is made up of one or more graphemes....
s making up the numerals are considered.
Bijective numeration systems
A bijective numeral system with base b uses b different numerals to represent all non-negative integers. However, the numerals have values 1, 2, 3, etc. up to and including b, whereas zero is represented by an empty digit string. For example it is possible to have decimal without a zero.Base one (unary numeral system)
Unary is the bijective numeral system with base b=1. In unary, one numeral is used to represent all positive integers. The value of the digit string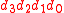 given by the polynomial form can be simplified into since 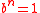for all n. Non-standard features of this system include:
- The value of a digit does not depend on its position. Thus, one can easily argue that unary is not a positional system at all.
- Introducing a radix point in this system will not enable representation of non-integer values.
- The single numeral represents the value 1, not the value 0=b-1.
- The value 0 cannot be represented (or is implicitly represented by an empty digit string).
Signed-digit representation
In some systems, while the base is a positive integer, negative digits are allowed. Non-adjacent formNon-adjacent form
The non-adjacent form of a number is a unique signed-digit representation. Like the name suggests, non-zero values cannot be adjacent. For example:2 = 4 + 2 + 1 = 72 = 8 − 2 + 1 = 72 = 8 − 4 + 2 + 1 = 72 = 8 − 1 = 7...
is a particular system where the base is b=2. In the balanced ternary
Balanced ternary
Balanced ternary is a non-standard positional numeral system , useful for comparison logic. It is a ternary system, but unlike the standard ternary system, the digits have the values −1, 0, and 1...
system, the base is b=3, and the numerals have the values −1, 0 and +1 (rather than 0, 1 and 2 as in the standard ternary system
Ternary numeral system
Ternary is the base- numeral system. Analogous to a bit, a ternary digit is a trit . One trit contains \log_2 3 bits of information...
, or 1, 2 and 3 as in the bijective ternary system).
Bases that are not positive integers
A few positional systems have been suggested in which the base b is not a positive integer.Negative base
Negative-base systems include negabinary, negaternary and negadecimal; in base −b the number of different numerals used is b. All integers, positive and negative, can be represented without a sign.Complex base
In purely imaginary base bi the b² numbers from 0 to b²-1 are used as digits.It can be generalized on other complex bases: Complex base systems
Complex base systems
In arithmetic, a complex base system is a positional numeral system whose radix is an imaginary or complex number In arithmetic, a complex base system is a positional numeral system whose radix is an imaginary (proposed by Donald Knuth in 1955) or complex number In arithmetic, a complex base...
.
Non-integer base
In these systems, the number of different numerals used clearly cannot be b. Example: Golden ratio baseGolden ratio base
Golden ratio base is a non-integer positional numeral system that uses the golden ratio as its base. It is sometimes referred to as base-φ, golden mean base, phi-base, or, colloquially, phinary...
(phinary).
Mixed bases
It is sometimes convenient to consider positional numeral systems where the weights associated with the positions do not form a geometric sequence 1, b, b2, b3, etc., starting from the least significant position, as given in the polynomial form. In a mixed radixMixed radix
Mixed radix numeral systems are non-standard positional numeral systems in which the numerical base varies from position to position. Such numerical representation applies when a quantity is expressed using a sequence of units that are each a multiple of the next smaller one, but not by the same...
system such as the factorial number system, the weights form a sequence where each weight is an integral multiple of the previous one. Other sequences can be used, but then every integer may not have a unique representation. For example, Fibonacci coding
Fibonacci coding
In mathematics, Fibonacci coding is a universal code which encodes positive integers into binary code words. Each code word ends with "11" and contains no other instances of "11" before the end.-Definition:...
uses the digits 0 and 1, weighted according to the Fibonacci sequence (1, 2, 3, 5, 8, ...); a unique representation of all non-negative integers may be ensured by forbidding consecutive 1's.
For calendrical use, the Mayan
Maya numerals
Maya Numerals were a vigesimal numeral system used by the Pre-Columbian Maya civilization.The numerals are made up of three symbols; zero , one and five...
numeral system was a mixed radix system, since one of its positions represents a multiplication by 18 rather than 20, in order to fit a 360-day calendar. Also, giving an angle in degrees, minutes and seconds (with decimals), or a time in days, hours, minutes and seconds, can be interpreted as mixed radix systems.