
Nonlocal Lagrangian
Encyclopedia
In field theory, a nonlocal Lagrangian is a Lagrangian
, a type of functional
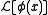 which contains terms which are nonlocal in the fields
which contains terms which are nonlocal in the fields 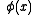 i.e. which are not polynomials or functions of the fields or their derivatives evaluated at a single point in the space of dynamical parameters (eg. space-time). Examples of such nonlocal Lagrangians might be
i.e. which are not polynomials or functions of the fields or their derivatives evaluated at a single point in the space of dynamical parameters (eg. space-time). Examples of such nonlocal Lagrangians might be

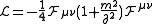

Actions
obtained from nonlocal Lagrangians are called nonlocal actions. The actions appearing in the fundamental theories of physics, such as the Standard Model
, are local actions - nonlocal actions play a part in theories which attempt to go beyond the Standard Model, and also appear in some effective field theories
. Nonlocalization of a local action is also an essential aspect of some regularization
procedures. Noncommutative quantum field theory
also gives rise to nonlocal actions.
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
, a type of functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
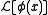 which contains terms which are nonlocal in the fields
which contains terms which are nonlocal in the fields 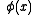 i.e. which are not polynomials or functions of the fields or their derivatives evaluated at a single point in the space of dynamical parameters (eg. space-time). Examples of such nonlocal Lagrangians might be
i.e. which are not polynomials or functions of the fields or their derivatives evaluated at a single point in the space of dynamical parameters (eg. space-time). Examples of such nonlocal Lagrangians might be
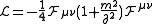

- The Wess–Zumino–Witten action
Actions
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
obtained from nonlocal Lagrangians are called nonlocal actions. The actions appearing in the fundamental theories of physics, such as the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, are local actions - nonlocal actions play a part in theories which attempt to go beyond the Standard Model, and also appear in some effective field theories
Effective field theory
In physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
. Nonlocalization of a local action is also an essential aspect of some regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
procedures. Noncommutative quantum field theory
Noncommutative quantum field theory
In mathematical physics, noncommutative quantum field theory is an application of noncommutative mathematics to the spacetime of quantum field theory that is an outgrowth of noncommutative geometry and index theory in which the coordinate functions are noncommutative...
also gives rise to nonlocal actions.

