Normal-exponential-gamma distribution
Encyclopedia
In probability theory
and statistics
, the normal-exponential-gamma distribution (sometimes called the NEG distribution) is a three-parameter family of continuous probability distribution
s. It has a location parameter
, scale parameter
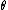and a shape parameter
.
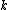(pdf) of the normal-exponential-gamma distribution distribution is proportional to
,
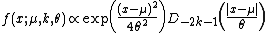where D is a parabolic cylinder function.
As for the Laplace distribution, the pdf of the NEG distribution can be expressed as a mixture of normal distributions,
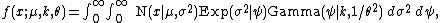
where, in this notation, the distribution-names should be interpreted as meaning the density functions of those distributions.
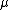and, because of this, it has applications in variable selection.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the normal-exponential-gamma distribution (sometimes called the NEG distribution) is a three-parameter family of continuous probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. It has a location parameter
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
, scale parameterScale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
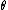and a shape parameterShape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
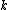.Probability density function
The probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(pdf) of the normal-exponential-gamma distribution distribution is proportional to
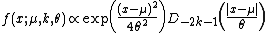,where D is a parabolic cylinder function.
As for the Laplace distribution, the pdf of the NEG distribution can be expressed as a mixture of normal distributions,
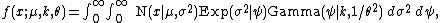
where, in this notation, the distribution-names should be interpreted as meaning the density functions of those distributions.
Applications
The distribution has heavy tails and a sharp peak at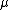 and, because of this, it has applications in variable selection.