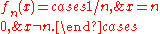Normal convergence
Encyclopedia
In mathematics
normal convergence is a type of convergence for series
of function
s. Like absolute-convergence
, it has the useful property that it is preserved when the order of summation is changed.
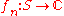 (or to any normed vector space
(or to any normed vector space
), the series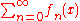
is called normally convergent if the series of uniform norms of the terms of the series convergeshttp://eom.springer.de/N/n067430.htm, i.e.,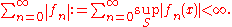
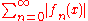 . To illustrate this, consider
. To illustrate this, consider
Then the series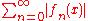 is uniformly convergent (for any ε take n ≥ 1/ε), but the series of uniform norms is the harmonic series
is uniformly convergent (for any ε take n ≥ 1/ε), but the series of uniform norms is the harmonic series
and thus diverges. An example using continuous functions can be made by replacing these functions with bump functions of height 1/n and width 1 centered at each natural number n.
As well, normal convergence of a series is different from norm-topology convergence, i.e. convergence of the partial sum sequence in the topology induced by the uniform norm. Normal convergence implies norm-topology convergence if and only iff the space of functions under consideration is complete
with respect to the uniform norm. (The converse does not hold even for complete function spaces: for example, consider the harmonic series as a sequence of constant functions).
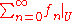
is normally convergent, i.e. such that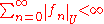
where the norm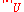 is the supremum over the domain U.
is the supremum over the domain U.

is normally convergent on K.
Note: if X is locally compact (even in the weakest sense), local normal convergence and compact normal convergence are equivalent.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
normal convergence is a type of convergence for series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. Like absolute-convergence
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
, it has the useful property that it is preserved when the order of summation is changed.
History
The concept of normal convergence was first introduced by René Baire in 1908 in his book Leçons sur les théories générales de l'analyse.Definition
Given a set S and functions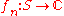 (or to any normed vector space
(or to any normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
), the series
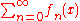
is called normally convergent if the series of uniform norms of the terms of the series convergeshttp://eom.springer.de/N/n067430.htm, i.e.,
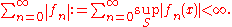
Distinctions
Normal convergence implies, but should not be confused with, uniform absolute convergence, i.e. uniform convergence of the series of nonnegative functions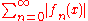 . To illustrate this, consider
. To illustrate this, considerThen the series
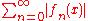 is uniformly convergent (for any ε take n ≥ 1/ε), but the series of uniform norms is the harmonic series
is uniformly convergent (for any ε take n ≥ 1/ε), but the series of uniform norms is the harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
and thus diverges. An example using continuous functions can be made by replacing these functions with bump functions of height 1/n and width 1 centered at each natural number n.
As well, normal convergence of a series is different from norm-topology convergence, i.e. convergence of the partial sum sequence in the topology induced by the uniform norm. Normal convergence implies norm-topology convergence if and only iff the space of functions under consideration is complete
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
with respect to the uniform norm. (The converse does not hold even for complete function spaces: for example, consider the harmonic series as a sequence of constant functions).
Local normal convergence
A series can be called "locally normally convergent on X" if each point x in X has a neighborhood U such that the series of functions fn restricted to the domain U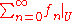
is normally convergent, i.e. such that
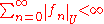
where the norm
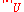 is the supremum over the domain U.
is the supremum over the domain U.Compact normal convergence
A series is said to be "normally convergent on compact subsets of X" or "compactly normally convergent on X" if for every compact subset K of X, the series of functions fn restricted to K
is normally convergent on K.
Note: if X is locally compact (even in the weakest sense), local normal convergence and compact normal convergence are equivalent.
Properties
- Every normal convergent series is uniformly convergent, locally uniformly convergent, and compactly uniformly convergent. This is very important, since it assures that any re-arrangement of the series, any derivatives or integrals of the series, and sums and products with other convergent series will converge to the "correct" value.
- If
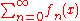 is normally convergent to
is normally convergent to  , then any re-arrangement of the sequence (f1, f2, f3 ...) also converges normally to the same f. That is, for every bijection
, then any re-arrangement of the sequence (f1, f2, f3 ...) also converges normally to the same f. That is, for every bijection  ,
, 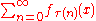 is normally convergent to
is normally convergent to  .
.