
Numerical sign problem
Encyclopedia
The numerical sign problem refers to the difficulty of numerically evaluating the integral of a highly oscillatory function of a large number of variables. Numerical methods fail because of the near-cancellation of the positive and negative contributions to the integral. Each has to be integrated to very high precision in order for their difference to be obtained with useful accuracy.
The sign problem is one of the major unsolved problems in the physics of many-particle systems. It often arises in calculations of the properties of a quantum mechanical system with large number of strongly-interacting fermions
, or in field theories involving a non-zero density of strongly-interacting fermions.
, or in field theories involving a non-zero density of strongly-interacting fermions. Because the particles are strongly interacting, perturbation theory
is inapplicable, and one is forced to use brute-force numerical methods. Because the particles are fermions, their wavefunction
changes sign when any two fermions are interchanged (due to the symmetry of the wave function, see Pauli principle). So unless there are cancellations arising from some symmetry of the system, the quantum-mechanical sum over all multi-particle states involves an integral over a function that is highly oscillatory, and hence hard to evaluate numerically, particularly in high dimension. Since the dimension of the integral is given by the number of particles, the sign problem becomes severe in the thermodynamic limit
. The field-theoretic manifestation of the sign problem is discussed below.
The sign problem is one of the major unsolved problems in the physics of many-particle systems, impeding progress in many areas:
In a field theory approach to multi-particle systems, the fermion density is controlled by the value of the fermion chemical potential
 . One evaluates the partition function
. One evaluates the partition function
 by summing over all classical field configurations, weighted by
by summing over all classical field configurations, weighted by 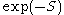 where
where 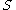 is the action of the configuration. The sum over fermion fields can be performed analytically, and one is left with a sum over the bosonic
is the action of the configuration. The sum over fermion fields can be performed analytically, and one is left with a sum over the bosonic
fields (which may have been originally part of the theory, or have been produced by a Hubbard-Stratonovich transformation
(which may have been originally part of the theory, or have been produced by a Hubbard-Stratonovich transformation
to make the fermion action quadratic)
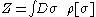
where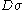 represents the measure for the sum over all configurations
represents the measure for the sum over all configurations 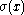 of the bosonic fields, weighted by
of the bosonic fields, weighted by
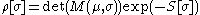
where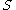 is now the action of the bosonic fields, and
is now the action of the bosonic fields, and 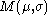 is a matrix that encodes how the fermions were coupled to the bosons. The expectation value of an observable
is a matrix that encodes how the fermions were coupled to the bosons. The expectation value of an observable  is therefore an average over all configurations weighted by
is therefore an average over all configurations weighted by 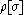

If is positive, then it can be interpreted as a probability measure, and
is positive, then it can be interpreted as a probability measure, and  can be calculated by performing the sum over field configurations numerically, using standard techniques such as Monte Carlo importance sampling.
can be calculated by performing the sum over field configurations numerically, using standard techniques such as Monte Carlo importance sampling.
The sign problem arises when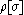 is non-positive. This typically occurs in theories of fermions when the fermion chemical potential
is non-positive. This typically occurs in theories of fermions when the fermion chemical potential 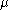 is nonzero, i.e. when there is a nonzero background density of fermions. If
is nonzero, i.e. when there is a nonzero background density of fermions. If 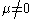 there is no particle-antiparticle symmetry, and
there is no particle-antiparticle symmetry, and 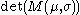 , and hence the weight
, and hence the weight 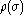 , is in general a complex number, so Monte-Carlo importance sampling cannot be used to evaluate the integral.
, is in general a complex number, so Monte-Carlo importance sampling cannot be used to evaluate the integral.

where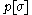 is real and positive, so
is real and positive, so
Note that the desired expectation value is now a ratio where the numerator and denominator are expectation values that both use a positive weighting function,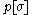 . However, the phase
. However, the phase 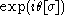 is a highly oscillatory function in the configuration space, so if one uses Monte-Carlo methods to evaluate the numerator and denominator, each of them will evaluate to a very small number, whose exact value is swamped by the noise inherent in the Monte-Carlo sampling process. The "badness" of the sign problem is measured by the smallness of the denominator
is a highly oscillatory function in the configuration space, so if one uses Monte-Carlo methods to evaluate the numerator and denominator, each of them will evaluate to a very small number, whose exact value is swamped by the noise inherent in the Monte-Carlo sampling process. The "badness" of the sign problem is measured by the smallness of the denominator 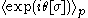 : if it is much less than 1 then the sign problem is severe.
: if it is much less than 1 then the sign problem is severe.
It can be shown (e.g. ) that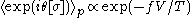
where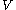 is the volume of the system,
is the volume of the system,  is the temperature, and
is the temperature, and  is an energy density. The number of Monte-Carlo sampling points needed to obtain an accurate result therefore rises exponentially as the volume of the system becomes large, and as the temperature goes to zero.
is an energy density. The number of Monte-Carlo sampling points needed to obtain an accurate result therefore rises exponentially as the volume of the system becomes large, and as the temperature goes to zero.
The decomposition of the weighting function in to modulus and phase is just one example (although it has been advocated as the optimal choice since it minimizes the variance of the denominator ). In general one could write
where can be any positive weighting function (for example, the weighting function of the
can be any positive weighting function (for example, the weighting function of the 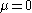 theory.) The badness of the sign problem is then measured by
theory.) The badness of the sign problem is then measured by
which again goes to zero exponentially in the large-volume limit.
, implying that a full and generic solution of the sign problem would also solve all problems in the complexity class NP in polynomial time . If (as is generally suspected) there are no polynomial-time solutions to NP-hard problems (see P versus NP problem), then there is no generic solution to the sign problem (on non-quantum computers). This leaves open the possibility that there may be solutions that work in specific cases, where the oscillations of the integrand have a structure that can be exploited to reduce the numerical errors.
In systems with a moderate sign problem, such as field theories at a sufficiently high temperature or in a sufficiently small volume, the sign problem is not too severe and useful results can be obtained by various methods, such as more carefully tuned reweighting, analytic continuation from imaginary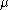 to real
to real 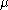 , or Taylor expansion in powers of
, or Taylor expansion in powers of  .
.
There are various proposals for solving systems with a severe sign problem:
The sign problem is one of the major unsolved problems in the physics of many-particle systems. It often arises in calculations of the properties of a quantum mechanical system with large number of strongly-interacting fermions
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
, or in field theories involving a non-zero density of strongly-interacting fermions.
The sign problem in physics
In physics, the sign problem is typically (but not exclusively) encountered in calculations of the properties of a quantum mechanical system with large number of strongly-interacting fermionsFermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
, or in field theories involving a non-zero density of strongly-interacting fermions. Because the particles are strongly interacting, perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
is inapplicable, and one is forced to use brute-force numerical methods. Because the particles are fermions, their wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
changes sign when any two fermions are interchanged (due to the symmetry of the wave function, see Pauli principle). So unless there are cancellations arising from some symmetry of the system, the quantum-mechanical sum over all multi-particle states involves an integral over a function that is highly oscillatory, and hence hard to evaluate numerically, particularly in high dimension. Since the dimension of the integral is given by the number of particles, the sign problem becomes severe in the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
. The field-theoretic manifestation of the sign problem is discussed below.
The sign problem is one of the major unsolved problems in the physics of many-particle systems, impeding progress in many areas:
- Condensed matter physics. It prevents the numerical solution of systems with a high density of strongly-correlated electrons, such as the Hubbard modelHubbard modelThe Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
. - Nuclear physics. It prevents the ab-initio calculation of properties of nuclear matterNuclear matterNuclear matter is an idealized system of interacting nucleons that exists in several phases that as yet are not fully established...
and hence limits our understanding of nucleiAtomic nucleusThe nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
and neutron starsNeutron starA neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
. - Particle physics. It prevents the use of Lattice QCDLattice QCDLattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time....
to predict the phases and properties of quark matter.
The sign problem in field theory
(References for this section: ,).In a field theory approach to multi-particle systems, the fermion density is controlled by the value of the fermion chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
 . One evaluates the partition function
. One evaluates the partition functionPartition function (quantum field theory)
In quantum field theory, we have a generating functional, Z[J] of correlation functions and this value, called the partition function is usually expressed by something like the following functional integral:...
 by summing over all classical field configurations, weighted by
by summing over all classical field configurations, weighted by 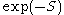 where
where 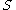 is the action of the configuration. The sum over fermion fields can be performed analytically, and one is left with a sum over the bosonic
is the action of the configuration. The sum over fermion fields can be performed analytically, and one is left with a sum over the bosonicBoson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
fields
 (which may have been originally part of the theory, or have been produced by a Hubbard-Stratonovich transformation
(which may have been originally part of the theory, or have been produced by a Hubbard-Stratonovich transformationHubbard-Stratonovich transformation
The Hubbard–Stratonovich transformation is an exact mathematical transformation invented by Russian physicist Ruslan L. Stratonovich and popularized by British physicist John Hubbard...
to make the fermion action quadratic)
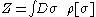
where
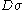 represents the measure for the sum over all configurations
represents the measure for the sum over all configurations 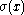 of the bosonic fields, weighted by
of the bosonic fields, weighted by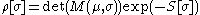
where
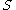 is now the action of the bosonic fields, and
is now the action of the bosonic fields, and 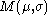 is a matrix that encodes how the fermions were coupled to the bosons. The expectation value of an observable
is a matrix that encodes how the fermions were coupled to the bosons. The expectation value of an observable  is therefore an average over all configurations weighted by
is therefore an average over all configurations weighted by 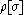

If
 is positive, then it can be interpreted as a probability measure, and
is positive, then it can be interpreted as a probability measure, and  can be calculated by performing the sum over field configurations numerically, using standard techniques such as Monte Carlo importance sampling.
can be calculated by performing the sum over field configurations numerically, using standard techniques such as Monte Carlo importance sampling.The sign problem arises when
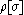 is non-positive. This typically occurs in theories of fermions when the fermion chemical potential
is non-positive. This typically occurs in theories of fermions when the fermion chemical potential 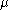 is nonzero, i.e. when there is a nonzero background density of fermions. If
is nonzero, i.e. when there is a nonzero background density of fermions. If 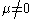 there is no particle-antiparticle symmetry, and
there is no particle-antiparticle symmetry, and 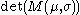 , and hence the weight
, and hence the weight 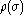 , is in general a complex number, so Monte-Carlo importance sampling cannot be used to evaluate the integral.
, is in general a complex number, so Monte-Carlo importance sampling cannot be used to evaluate the integral.Reweighting procedure
A field theory with a non-positive weight can be transformed to one with a positive weight, by incorporating the non-positive part (sign or complex phase) of the weight in to the observable. For example, one could decompose the weighting function in to its modulus and phase,
where
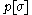 is real and positive, so
is real and positive, so
Note that the desired expectation value is now a ratio where the numerator and denominator are expectation values that both use a positive weighting function,
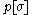 . However, the phase
. However, the phase 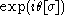 is a highly oscillatory function in the configuration space, so if one uses Monte-Carlo methods to evaluate the numerator and denominator, each of them will evaluate to a very small number, whose exact value is swamped by the noise inherent in the Monte-Carlo sampling process. The "badness" of the sign problem is measured by the smallness of the denominator
is a highly oscillatory function in the configuration space, so if one uses Monte-Carlo methods to evaluate the numerator and denominator, each of them will evaluate to a very small number, whose exact value is swamped by the noise inherent in the Monte-Carlo sampling process. The "badness" of the sign problem is measured by the smallness of the denominator 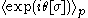 : if it is much less than 1 then the sign problem is severe.
: if it is much less than 1 then the sign problem is severe.It can be shown (e.g. ) that
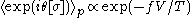
where
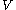 is the volume of the system,
is the volume of the system,  is the temperature, and
is the temperature, and  is an energy density. The number of Monte-Carlo sampling points needed to obtain an accurate result therefore rises exponentially as the volume of the system becomes large, and as the temperature goes to zero.
is an energy density. The number of Monte-Carlo sampling points needed to obtain an accurate result therefore rises exponentially as the volume of the system becomes large, and as the temperature goes to zero.The decomposition of the weighting function in to modulus and phase is just one example (although it has been advocated as the optimal choice since it minimizes the variance of the denominator ). In general one could write

where
 can be any positive weighting function (for example, the weighting function of the
can be any positive weighting function (for example, the weighting function of the 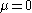 theory.) The badness of the sign problem is then measured by
theory.) The badness of the sign problem is then measured by
which again goes to zero exponentially in the large-volume limit.
Methods for reducing the sign problem
The sign problem is NP-hardNP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
, implying that a full and generic solution of the sign problem would also solve all problems in the complexity class NP in polynomial time . If (as is generally suspected) there are no polynomial-time solutions to NP-hard problems (see P versus NP problem), then there is no generic solution to the sign problem (on non-quantum computers). This leaves open the possibility that there may be solutions that work in specific cases, where the oscillations of the integrand have a structure that can be exploited to reduce the numerical errors.
In systems with a moderate sign problem, such as field theories at a sufficiently high temperature or in a sufficiently small volume, the sign problem is not too severe and useful results can be obtained by various methods, such as more carefully tuned reweighting, analytic continuation from imaginary
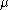 to real
to real 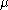 , or Taylor expansion in powers of
, or Taylor expansion in powers of  .
. There are various proposals for solving systems with a severe sign problem:
- Meron-cluster algorithms. These achieve an exponential speed-up by decomposing the fermion world lines in to clusters that contribute independently. Cluster algorithms have been developed for certain theories , but not for the Hubbard model of electrons, nor for QCDQCDThe initialism QCD may refer to:* Quantum chromodynamics, the theory describing the Strong Interaction* Quantum circuit diagram* Quality, Cost, Delivery, a three-letter acronym used in lean manufacturing...
, the theory of quarks.
- Stochastic quantization. The sum over configurations is obtained as the equilibrium distribution of states explored by a complex Langevin equationLangevin equationIn statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
. So far, the algorithm has been found to evade the sign problem in test models that have a sign problem but do not involve fermions. .
- Fixed Node method. One fixes the location of nodes (zeros) of the multiparticle wavefunction, and uses Monte-Carlo methods to obtain an estimate of the energy of the ground state, subject to that constraint.

