Néron–Severi group
Encyclopedia
In algebraic geometry
, the Néron–Severi group of a variety
is
the group of divisors modulo algebraic equivalence; in other words it is the group of components
of the Picard scheme of a variety. Its rank is called the Picard number. It is named after Francesco Severi
and André Néron
.
of the Picard scheme is an abelian variety
written
and the quotient
is an abelian group NS(V), called the Néron–Severi group of V. This is
a finitely-generated abelian group by the Néron–Severi theorem, which was proved by Severi over the complex numbers and by Néron over more general fields.
In other words the Picard group fits into an exact sequence
The fact that the rank is finite is Francesco Severi
's theorem of the base; the rank is the Picard number of V, often denoted ρ(V). The elements of finite order are called Severi divisors, and form a finite group which is a birational invariant and whose order is called the Severi number. Geometrically NS(V) describes the algebraic equivalence classes of divisors
on V; that is, using a stronger, non-linear equivalence relation in place of linear equivalence of divisors, the classification becomes amenable to discrete invariants. Algebraic equivalence is closely related to numerical equivalence, an essentially topological classification by intersection number
s.
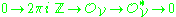gives rise to a long exact sequence featuring 
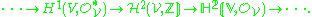The first arrow is the first Chern class on the Picard group
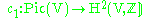, and the second 
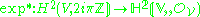. The Neron-Severi group can be identified with the image of the first Chern class, or equivalently, by exactness, as the kernel of the second arrow 
.
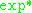In the complex case, the Neron-Severi group is therefore the group of 2-cocycles whose Poincaré dual is represented by a complex hypersurface, that is, a Weil divisor.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Néron–Severi group of a variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
is
the group of divisors modulo algebraic equivalence; in other words it is the group of components
Component (group theory)
In mathematics, in the field of group theory, a component of a finite group is a quasisimple subnormal subgroup. Any two distinct components commute...
of the Picard scheme of a variety. Its rank is called the Picard number. It is named after Francesco Severi
Francesco Severi
Francesco Severi was an Italian mathematician.Severi was born in Arezzo, Italy. He is famous for his contributions to algebraic geometry and the theory of functions of several complex variables. He became the effective leader of the Italian school of algebraic geometry...
and André Néron
André Néron
André Néron was a French mathematician at the Université de Poitiers who worked on elliptic curves and Abelian varieties...
.
Definition
In the cases of most importance to classical algebraic geometry, for a complete variety V that is non-singular, the connected componentConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of the Picard scheme is an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
written
- Pic0(V)
and the quotient
- Pic(V)/Pic0(V)
is an abelian group NS(V), called the Néron–Severi group of V. This is
a finitely-generated abelian group by the Néron–Severi theorem, which was proved by Severi over the complex numbers and by Néron over more general fields.
In other words the Picard group fits into an exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
The fact that the rank is finite is Francesco Severi
Francesco Severi
Francesco Severi was an Italian mathematician.Severi was born in Arezzo, Italy. He is famous for his contributions to algebraic geometry and the theory of functions of several complex variables. He became the effective leader of the Italian school of algebraic geometry...
's theorem of the base; the rank is the Picard number of V, often denoted ρ(V). The elements of finite order are called Severi divisors, and form a finite group which is a birational invariant and whose order is called the Severi number. Geometrically NS(V) describes the algebraic equivalence classes of divisors
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
on V; that is, using a stronger, non-linear equivalence relation in place of linear equivalence of divisors, the classification becomes amenable to discrete invariants. Algebraic equivalence is closely related to numerical equivalence, an essentially topological classification by intersection number
Intersection number
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency...
s.
First Chern class and integral valued 2-cocycles
The exponential sheaf sequenceExponential sheaf sequence
In mathematics, the exponential sheaf sequence is a fundamental short exact sequence of sheaves used in complex geometry.Let M be a complex manifold, and write OM for the sheaf of holomorphic functions on M. Let OM* be the subsheaf consisting of the non-vanishing holomorphic functions. These are...
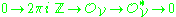gives rise to a long exact sequence featuring 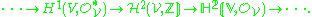The first arrow is the first Chern class on the Picard group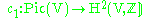, and the second 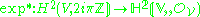. The Neron-Severi group can be identified with the image of the first Chern class, or equivalently, by exactness, as the kernel of the second arrow .In the complex case, the Neron-Severi group is therefore the group of 2-cocycles whose Poincaré dual is represented by a complex hypersurface, that is, a Weil divisor.