
Oblique reflection
Encyclopedia
In Euclidean geometry
, oblique reflections generalize ordinary reflections
by not requiring that reflection be done using perpendicular
s. If two points are oblique reflections of each other, they will still stay so under affine transformation
s.
Consider a plane P in the three-dimensional Euclidean space
. The usual reflection of a point A in space in respect to the plane P is another point B in space, such that the midpoint of the segment AB is in the plane, and AB is perpendicular to the plane. For an oblique reflection, one requires instead of perpendicularity that AB be parallel to a given reference line.
Formally, let there be a plane P in the three-dimensional space, and a line L in space not parallel to P. To obtain the oblique reflection of a point A in space in respect to the plane P, one draws through A a line parallel to L, and lets the oblique reflection of A be the point B on that line on the other side of the plane such that the midpoint of AB is in P. If the reference line L is perpendicular to the plane, one obtains the usual reflection.
For example, consider the plane P to be the xy plane, that is, the plane given by the equation z=0 in Cartesian coordinates. Let the direction of the reference line L be given by the vector (a, b, c), with c≠0 (that is, L is not parallel to P). The oblique reflection of a point (x, y, z) will then be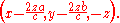
The concept of oblique reflection is easily generalizable to oblique reflection in respect to an affine hyperplane in Rn with a line again serving as a reference, or even more generally, oblique reflection in respect to a k-dimensional affine subspace, with a n−k-dimensional affine subspace serving as a reference. Back to three dimensions, one can then define oblique reflection in respect to a line, with a plane serving as a reference.
An oblique reflection is an affine transformation
, and it is an involution, meaning that the reflection of the reflection of a point is the point itself.
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, oblique reflections generalize ordinary reflections
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
by not requiring that reflection be done using perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
s. If two points are oblique reflections of each other, they will still stay so under affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s.
Consider a plane P in the three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The usual reflection of a point A in space in respect to the plane P is another point B in space, such that the midpoint of the segment AB is in the plane, and AB is perpendicular to the plane. For an oblique reflection, one requires instead of perpendicularity that AB be parallel to a given reference line.
Formally, let there be a plane P in the three-dimensional space, and a line L in space not parallel to P. To obtain the oblique reflection of a point A in space in respect to the plane P, one draws through A a line parallel to L, and lets the oblique reflection of A be the point B on that line on the other side of the plane such that the midpoint of AB is in P. If the reference line L is perpendicular to the plane, one obtains the usual reflection.
For example, consider the plane P to be the xy plane, that is, the plane given by the equation z=0 in Cartesian coordinates. Let the direction of the reference line L be given by the vector (a, b, c), with c≠0 (that is, L is not parallel to P). The oblique reflection of a point (x, y, z) will then be
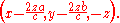
The concept of oblique reflection is easily generalizable to oblique reflection in respect to an affine hyperplane in Rn with a line again serving as a reference, or even more generally, oblique reflection in respect to a k-dimensional affine subspace, with a n−k-dimensional affine subspace serving as a reference. Back to three dimensions, one can then define oblique reflection in respect to a line, with a plane serving as a reference.
An oblique reflection is an affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
, and it is an involution, meaning that the reflection of the reflection of a point is the point itself.

