
Omega-categorical theory
Encyclopedia
In mathematical logic
, an omega-categorical theory is a theory
that has only one countable
model up to
isomorphism
. Omega-categoricity is the special case κ =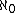 = ω of κ-categoricity
= ω of κ-categoricity
, and omega-categorical theories are also referred to as ω-categorical. The notion is most important for countable first-order
theories.
, Czesław Ryll-Nardzewski and Lars Svenonius
, proved several independently. Despite this, the literature still widely refers to the Ryll-Nardzewski theorem as a name for these conditions. The conditions included with the theorem vary between authors.
Given a countable complete
first-order theory T with infinite models, the following are equivalent:
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, an omega-categorical theory is a theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
that has only one countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
model up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. Omega-categoricity is the special case κ =
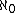 = ω of κ-categoricity
= ω of κ-categoricityMorley's categoricity theorem
In model theory, a branch of mathematical logic, a theory is κ-categorical if it has exactly one model of cardinality κ up to isomorphism....
, and omega-categorical theories are also referred to as ω-categorical. The notion is most important for countable first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
theories.
Equivalent conditions for omega-categoricity
Many conditions on a theory are equivalent to the property of omega-categoricity. In 1959 Erwin EngelerErwin Engeler
Erwin Engeler is a Swiss mathematician who did pioneering work on the interrelations between logic, computer science and scientific computation in the 20th century...
, Czesław Ryll-Nardzewski and Lars Svenonius
Lars Svenonius
Lars Svenonius was a Swedish logician and philosopher.He was a visiting professor at University of California at Berkeley in 1962-63, then held a position at the University of Chicago from 1963-69, and was professor of philosophy at the University of Maryland from 1969 to 2009...
, proved several independently. Despite this, the literature still widely refers to the Ryll-Nardzewski theorem as a name for these conditions. The conditions included with the theorem vary between authors.
Given a countable complete
Complete theory
In mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
first-order theory T with infinite models, the following are equivalent:
- The theory T is omega-categorical.
- Every countable model of T has an oligomorphic automorphism groupOligomorphic groupIn group theory, a branch of mathematics, an oligomorphic group is a particular kind of permutation group. If a group G acts on a set S, then G is said to be oligomorphic if every Cartesian product, Sn of S has finitely many orbits under the action of G...
. - Some countable model of T has an oligomorphic automorphism group.
- The theory T has a model which, for every natural number n, realizes only finitely many n-types, that is, the Stone space Sn(T) is finite.
- For every natural number n, T has only finitely many n-types.
- For every natural number n, every n-type is isolated.
- For every natural number n, up to equivalence modulo T there are only finitely many formulas with n free variables, in other words, every nth Lindenbaum-Tarski algebra of T is finite.
- Every model of T is atomic.
- Every countable model of T is atomic.
- The theory T has a countable atomic and saturated modelSaturated modelIn mathematical logic, and particularly in its subfield model theory, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size...
. - The theory T has a saturated prime modelPrime modelIn mathematics, and in particular model theory, a prime model is a model which is as simple as possible. Specifically, a model P is prime if it admits an elementary embedding into any model M to which it is elementarily equivalent .- Cardinality :In contrast with the notion of saturated model,...
.

