
On the Sphere and Cylinder
Encyclopedia
On the Sphere and Cylinder is a work that was published by Archimedes
in two volumes c. 225 BC. It most notably details how to find the surface area
of a sphere
and the volume of the contained ball
and the analogous values for a cylinder
, and was the first to do so.
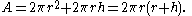
and that the volume of the same is:
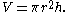
On the sphere, he showed that the surface area is four times the area of its great circle
. In modern terms, this means that the surface area is equal to:
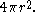
The result for the volume of the contained ball stated that it is two-thirds the volume of a circumscribed cylinder
, meaning that the volume is
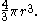
Archimedes was particularly proud of this latter result, and so he asked for a sketch of a sphere inscribed in a cylinder to be inscribed on his grave - he had shown that both the volume and the surface area of the sphere were two-thirds that of the cylinder. Later, Roman
philosopher
Marcus Tullius Cicero
discovered the tomb, which had been overgrown by surrounding vegetation.
The argument Archimedes used to prove the formula for the volume of a ball was rather involved in its geometry, and many modern textbooks have a simplified version using the concept of a limit
, which, of course, did not exist in Archimedes' time. Archimedes used an inscribed half-polygon in a semicircle, then rotated both to create a conglomerate of frustum
s in a sphere, of which he then determined the volume.
It seems that this is not the original method Archimedes used to derive this result, but the best formal argument available to him in the Greek mathematical tradition. His original method likely involved a clever use of levers. A palimsest
rediscovered in the 19th century contained many of Archimedes works, including The Method of Mechanical Theorems, in which he describes a method to determine volumes which involves balances, centers of mass and infinitesimal slices .
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
in two volumes c. 225 BC. It most notably details how to find the surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
and the volume of the contained ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
and the analogous values for a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
, and was the first to do so.
Contents
The principal formulae derived in On the Sphere and Cylinder are those mentioned above: the surface area of the sphere, the volume of the contained ball, and surface area and volume of the cylinder. In his work, Archimedes showed that the surface area of a cylinder is equal to: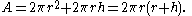
and that the volume of the same is:
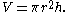
On the sphere, he showed that the surface area is four times the area of its great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
. In modern terms, this means that the surface area is equal to:
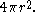
The result for the volume of the contained ball stated that it is two-thirds the volume of a circumscribed cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
, meaning that the volume is
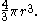
Archimedes was particularly proud of this latter result, and so he asked for a sketch of a sphere inscribed in a cylinder to be inscribed on his grave - he had shown that both the volume and the surface area of the sphere were two-thirds that of the cylinder. Later, Roman
Ancient Rome
Ancient Rome was a thriving civilization that grew on the Italian Peninsula as early as the 8th century BC. Located along the Mediterranean Sea and centered on the city of Rome, it expanded to one of the largest empires in the ancient world....
philosopher
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
Marcus Tullius Cicero
Cicero
Marcus Tullius Cicero , was a Roman philosopher, statesman, lawyer, political theorist, and Roman constitutionalist. He came from a wealthy municipal family of the equestrian order, and is widely considered one of Rome's greatest orators and prose stylists.He introduced the Romans to the chief...
discovered the tomb, which had been overgrown by surrounding vegetation.
The argument Archimedes used to prove the formula for the volume of a ball was rather involved in its geometry, and many modern textbooks have a simplified version using the concept of a limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
, which, of course, did not exist in Archimedes' time. Archimedes used an inscribed half-polygon in a semicircle, then rotated both to create a conglomerate of frustum
Frustum
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
s in a sphere, of which he then determined the volume.
It seems that this is not the original method Archimedes used to derive this result, but the best formal argument available to him in the Greek mathematical tradition. His original method likely involved a clever use of levers. A palimsest
Archimedes Palimpsest
The Archimedes Palimpsest is a palimpsest on parchment in the form of a codex. It originally was a copy of an otherwise unknown work of the ancient mathematician, physicist, and engineer Archimedes of Syracuse and other authors, which was overwritten with a religious text.Archimedes lived in the...
rediscovered in the 19th century contained many of Archimedes works, including The Method of Mechanical Theorems, in which he describes a method to determine volumes which involves balances, centers of mass and infinitesimal slices .

