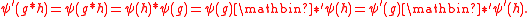Opposite group
Encyclopedia
In group theory
, a branch of mathematics
, an opposite group is a way to construct a group from another group that allows one to define right action
as a special case of left action.
 be a group under the operation
be a group under the operation  . The opposite group of
. The opposite group of  , denoted
, denoted 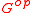 , has the same underlying set as
, has the same underlying set as  , and its group operation
, and its group operation  is defined by
is defined by 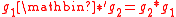 .
.
If is abelian, then it is equal to its opposite group. Also, every group
is abelian, then it is equal to its opposite group. Also, every group  (not necessarily abelian) is isomorphic to its opposite group: An isomorphism
(not necessarily abelian) is isomorphic to its opposite group: An isomorphism  is given by
is given by  . More generally, any anti-automorphism
. More generally, any anti-automorphism  gives rise to a corresponding isomorphism
gives rise to a corresponding isomorphism  via
via 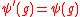 , since
, since
 be an object in some category, and
be an object in some category, and  be a right action
be a right action
. Then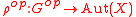 is a left action defined by
is a left action defined by 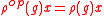 , or
, or 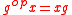 .
.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an opposite group is a way to construct a group from another group that allows one to define right action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
as a special case of left action.
Definition
Let be a group under the operation
be a group under the operation  . The opposite group of
. The opposite group of  , denoted
, denoted 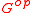 , has the same underlying set as
, has the same underlying set as  , and its group operation
, and its group operation  is defined by
is defined by 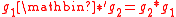 .
.If
 is abelian, then it is equal to its opposite group. Also, every group
is abelian, then it is equal to its opposite group. Also, every group  (not necessarily abelian) is isomorphic to its opposite group: An isomorphism
(not necessarily abelian) is isomorphic to its opposite group: An isomorphism  is given by
is given by  . More generally, any anti-automorphism
. More generally, any anti-automorphism  gives rise to a corresponding isomorphism
gives rise to a corresponding isomorphism  via
via 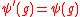 , since
, since
Group action
Let be an object in some category, and
be an object in some category, and  be a right action
be a right actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. Then
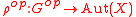 is a left action defined by
is a left action defined by 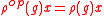 , or
, or 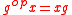 .
.