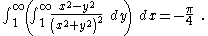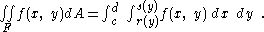.gif)
Order of integration (calculus)
Encyclopedia
In calculus
, interchange of the order of integration is a methodology that transforms iterated integral
s (or multiple integrals through the use of Fubini's theorem
) of functions into other, hopefully simpler, integrals by changing the order in which the integrations are performed. In some cases, the order of integration can be validly interchanged; in others it cannot.
where D is some two-dimensional area in the xy–plane. For some functions f straightforward integration is feasible, but where that is not true, the integral can sometimes be reduced to simpler form by changing the order of integration. The difficulty with this interchange is determining the change in description of the domain D.
The method also is applicable to multiple integrals.
Sometimes, even though a full evaluation is difficult, or perhaps requires a numerical integration, a double integral can be reduced to a single integration, as illustrated next. Reduction to a single integration makes a numerical evaluation
much easier and more efficient.
 Consider the iterated integral
Consider the iterated integral
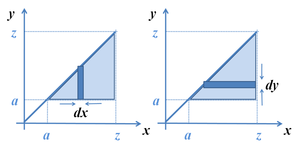
In this expression, the second integral is calculated first with respect to y and x is held constant—a strip of width dx is integrated first over the y-direction (a strip of width dx in the x direction is integrated with respect to the y variable across the y direction), adding up an infinite amount of rectangles of width dy along the y-axis. This forms a three dimensional slice dx wide along the x-axis, from y=a to y=x along the y axis, and in the z direction z=f(x,y). Notice that if the thickness dx is infinitesimal, x varies only infinitesimally on the slice. We can assume that x is constant. This integration is as shown in the left panel of Figure 1, but is inconvenient especially when the function h ( y ) is not easily integrated. The integral can be reduced to a single integration by reversing the order of integration as shown in the right panel of the figure. To accomplish this interchange of variables, the strip of width dy is first integrated from the line x = y to the limit x = z, and then the result is integrated from y = a to y = z, resulting in:
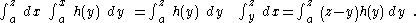
This result can be seen to be an example of the formula for integration by parts
, as stated below:
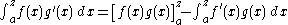
Substitute:
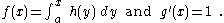
Which gives the result.
, see Whittaker and Watson, Gakhov, Lu, or Zwillinger. See also the discussion of the Poincaré-Bertrand transformation in Obolashvili. An example where the order of integration cannot be exchanged is given by Kanwal:
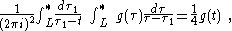
while:

The second form is evaluated using a partial fraction
expansion and an evaluation using the Sokhotski-Plemelj formula:
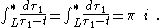
The notation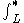 indicates a Cauchy principal value
indicates a Cauchy principal value
. See Kanwal.

Two basic theorems governing admissibility of the interchange are quoted below from Chaudhry and Zubair:
The most important theorem for the applications is quoted from Protter and Morrey:
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, interchange of the order of integration is a methodology that transforms iterated integral
Iterated integral
In calculus an iterated integral is the result of applying integrals to a function of more than one variable in a way that each of the integrals considers some of the variables as given constants. For example, the function f, if y is considered a given parameter can be integrated with respect to...
s (or multiple integrals through the use of Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
) of functions into other, hopefully simpler, integrals by changing the order in which the integrations are performed. In some cases, the order of integration can be validly interchanged; in others it cannot.
Problem statement
The problem for examination is evaluation of an integral of the form: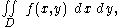
where D is some two-dimensional area in the xy–plane. For some functions f straightforward integration is feasible, but where that is not true, the integral can sometimes be reduced to simpler form by changing the order of integration. The difficulty with this interchange is determining the change in description of the domain D.
The method also is applicable to multiple integrals.
Sometimes, even though a full evaluation is difficult, or perhaps requires a numerical integration, a double integral can be reduced to a single integration, as illustrated next. Reduction to a single integration makes a numerical evaluation
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
much easier and more efficient.
Relation to integration by parts


In this expression, the second integral is calculated first with respect to y and x is held constant—a strip of width dx is integrated first over the y-direction (a strip of width dx in the x direction is integrated with respect to the y variable across the y direction), adding up an infinite amount of rectangles of width dy along the y-axis. This forms a three dimensional slice dx wide along the x-axis, from y=a to y=x along the y axis, and in the z direction z=f(x,y). Notice that if the thickness dx is infinitesimal, x varies only infinitesimally on the slice. We can assume that x is constant. This integration is as shown in the left panel of Figure 1, but is inconvenient especially when the function h ( y ) is not easily integrated. The integral can be reduced to a single integration by reversing the order of integration as shown in the right panel of the figure. To accomplish this interchange of variables, the strip of width dy is first integrated from the line x = y to the limit x = z, and then the result is integrated from y = a to y = z, resulting in:
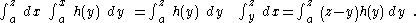
This result can be seen to be an example of the formula for integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
, as stated below:
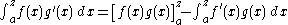
Substitute:
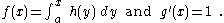
Which gives the result.
Principal-value integrals
For application to principal-value integralsCauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
, see Whittaker and Watson, Gakhov, Lu, or Zwillinger. See also the discussion of the Poincaré-Bertrand transformation in Obolashvili. An example where the order of integration cannot be exchanged is given by Kanwal:
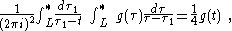
while:

The second form is evaluated using a partial fraction
Partial fractions in integration
In integral calculus, partial fraction expansions provide an approach to integrating a general rational function. Any rational function of a real variable can be written as the sum of a polynomial function and a finite number of algebraic fractions...
expansion and an evaluation using the Sokhotski-Plemelj formula:
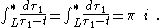
The notation
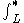 indicates a Cauchy principal value
indicates a Cauchy principal valueCauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
. See Kanwal.
Basic theorems
A good discussion of the basis for reversing the order of integration is found in Körner. He introduces his discussion with an example where interchange of integration leads to two different answers because the conditions of Theorem II below are not satisfied. Here is the example:
Two basic theorems governing admissibility of the interchange are quoted below from Chaudhry and Zubair:
The most important theorem for the applications is quoted from Protter and Morrey:
Suppose F is a region given bywhere p and q are continuous and p(x) ≤ q(x) for a ≤ x ≤ b. Suppose that f(x, y) is continuous on F. Then
The corresponding result holds if the closed region F has the representationwhere r(y) ≤ s(y) for c ≤ y ≤ d. In such a case,
External links
- Paul's Online Math Notes: Calculus III
- http://www.math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/vcalc/255doub/255doub.html Good 3D images showing the computation of "Double Integrals" using iterated integrals in the Department of Mathematics at Oregon State University.
- Ron Miech's UCLA Calculus Problems More complex examples of changing the order of integration (see Problems 33, 35, 37, 39, 41 & 43)
- Duane Nykamp's University of Minnesota website
- http://books.google.com/books?id=Q0Pvv4vWOlQC&pg=PA663&dq=%22order+of+integration%22&lr=&as_brr=0&sig=mpTlgi1ymBFa5AesR3AtwiPHKR8 A general introduction.