Orthogonal trajectory
Encyclopedia
In mathematics
, orthogonal trajectories are a family of curves in the plane that intersect a given family of curves at right angle
s. The problem is classical, but is now understood by means of complex analysis
; see for example harmonic conjugate
.
For a family of level curves described by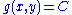
, where 
is a constant, the orthogonal trajectories may be found as the level curves of a new function 
by solving the partial differential equation
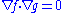
for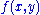
. This is literally a statement that the gradient
s of the functions (which are perpendicular to the curves) are orthogonal. Note that if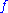
and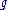 
are functions of three variables instead of two, the equation above will be nonlinear and will specify orthogonal surface
s.
The partial differential equation may be avoided by instead equating the tangent of a parametric curve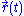
with the gradient of 
:
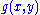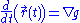
which will result in two possibly coupled ordinary differential equations, whose solutions are the orthogonal trajectories. Note that with this formula, if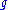
is a function of three variables its level set
s are surfaces, and the family of curves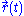
are orthogonal to the surfaces.
where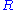
is the radius of the circle. Then the orthogonal trajectories are the level curves of 
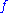defined by:
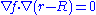
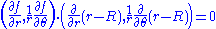
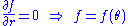
The lack of complete boundary data prevents determining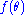
. However, we want our orthogonal trajectories to span every point on every circle, which means that 
must have a range which at least include one period of rotation. Thus, the level curves of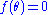 
, with freedom to choose any 
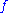, are all of the 
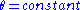curves that intersect circles, which are (all of the) straight lines passing through the origin. Note that the dot product
takes nearly the familiar form since polar coordinates are orthogonal
.
The absence of boundary data is a good thing, as it makes solving the PDE simple as one doesn't need to contort the solution to any boundary. In general, though, it must be ensured that all of the trajectories are found.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, orthogonal trajectories are a family of curves in the plane that intersect a given family of curves at right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s. The problem is classical, but is now understood by means of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
; see for example harmonic conjugate
Harmonic conjugate
In mathematics, a function u defined on some open domain \Omega\subset\R^2 is said to have as a conjugate a function v if and only if they are respectively real and imaginary part of a holomorphic function f of the complex variable z:=x+iy\in\Omega. That is, v is conjugated to u if f:=u+iv is...
.
For a family of level curves described by
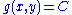, where is a constant, the orthogonal trajectories may be found as the level curves of a new function by solving the partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
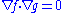
for
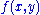. This is literally a statement that the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
s of the functions (which are perpendicular to the curves) are orthogonal. Note that if
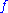and 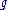are functions of three variables instead of two, the equation above will be nonlinear and will specify orthogonal surfaceSurface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s.
The partial differential equation may be avoided by instead equating the tangent of a parametric curve
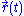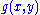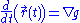
with the gradient of :which will result in two possibly coupled ordinary differential equations, whose solutions are the orthogonal trajectories. Note that with this formula, if
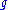is a function of three variables its level setLevel set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
s are surfaces, and the family of curves
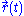are orthogonal to the surfaces.Example: circle
In polar coordinates, the family of circles centered about the origin is the level curves ofwhere
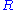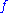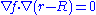
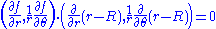
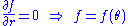
is the radius of the circle. Then the orthogonal trajectories are the level curves of defined by:The lack of complete boundary data prevents determining
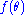. However, we want our orthogonal trajectories to span every point on every circle, which means that must have a range which at least include one period of rotation. Thus, the level curves of 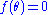, with freedom to choose any 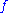, are all of the 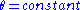curves that intersect circles, which are (all of the) straight lines passing through the origin. Note that the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
takes nearly the familiar form since polar coordinates are orthogonal
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
The absence of boundary data is a good thing, as it makes solving the PDE simple as one doesn't need to contort the solution to any boundary. In general, though, it must be ensured that all of the trajectories are found.
External links
- Exploring orthogonal trajectories - applet allowing user to draw families of curves and their orthogonal trajectories.