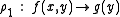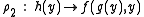Orthogonality (term rewriting)
Encyclopedia
Orthogonality as a property of term rewriting systems describes where the reduction rules of the system are all left-linear, that is each variable occurs only once on the left hand side of each reduction rule, and there is no overlap
between them.
Orthogonal term rewriting systems have the consequent property that all reducible expressions (redexes) within a term are completely disjoint -- that is, the redexes share no common function symbol.
For example, the term rewriting system with reduction rules
is orthogonal -- it is easy to observe that each reduction rule is left-linear, and the left hand side of each reduction rule shares no function symbol in common, so there is no overlap.
Orthogonal term rewriting systems are confluent
.
Overlap (term rewriting)
In mathematics, computer science and logic, overlap, as a property of the reduction rules in term rewriting system, describes a situation where a number of different reduction rules specify potentially contradictory ways of reducing a reducible expression within a term...
between them.
Orthogonal term rewriting systems have the consequent property that all reducible expressions (redexes) within a term are completely disjoint -- that is, the redexes share no common function symbol.
For example, the term rewriting system with reduction rules
is orthogonal -- it is easy to observe that each reduction rule is left-linear, and the left hand side of each reduction rule shares no function symbol in common, so there is no overlap.
Orthogonal term rewriting systems are confluent
Confluence (term rewriting)
In computer science, confluence is a property of rewriting systems, describing that terms in this system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system.- Motivating example :Consider...
.