
Overfull graph
Encyclopedia
In graph theory
, an overfull graph is a graph whose size is greater than the product of its maximum degree and its order floored, i.e.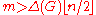 where m is the size of G,
where m is the size of G,  is the maximum degree of G, and n is the order of G. The concept of an overfull subgraph, an overfull graph that is a subgraph, immediately follows. An alternate, stricter definition of an overfull subgraph S of a graph G requires
is the maximum degree of G, and n is the order of G. The concept of an overfull subgraph, an overfull graph that is a subgraph, immediately follows. An alternate, stricter definition of an overfull subgraph S of a graph G requires 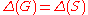 .
.
This conjecture, if true, would have numerous implications in graph theory, including the 1-factorization conjecture.
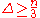 , there are at most three induced overfull subgraphs, and it is possible to find an overfull subgraph in polynomial time. When
, there are at most three induced overfull subgraphs, and it is possible to find an overfull subgraph in polynomial time. When 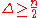 , there is at most one induced overfull subgraph, and it is possible to find it in linear time.
, there is at most one induced overfull subgraph, and it is possible to find it in linear time.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an overfull graph is a graph whose size is greater than the product of its maximum degree and its order floored, i.e.
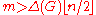 where m is the size of G,
where m is the size of G,  is the maximum degree of G, and n is the order of G. The concept of an overfull subgraph, an overfull graph that is a subgraph, immediately follows. An alternate, stricter definition of an overfull subgraph S of a graph G requires
is the maximum degree of G, and n is the order of G. The concept of an overfull subgraph, an overfull graph that is a subgraph, immediately follows. An alternate, stricter definition of an overfull subgraph S of a graph G requires 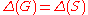 .
.Properties
A few properties of overfull graphs:- Overfull graphs are of odd order.
- Overfull graphs are class 2. That is, they require at least colors in any edge coloringEdge coloringIn graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
. - A graph G, with an overfull subgraph S such that
 , is of class 2.
, is of class 2.
Overfull conjecture
In 1986, Chetwynd and Hilton posited the following conjecture that is now known as the overfull conjecture.- A graph G with
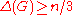 is class 2 if and only if it has an overfull subgraph S such that
is class 2 if and only if it has an overfull subgraph S such that 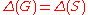 .
.
This conjecture, if true, would have numerous implications in graph theory, including the 1-factorization conjecture.
Algorithms
For graphs in which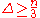 , there are at most three induced overfull subgraphs, and it is possible to find an overfull subgraph in polynomial time. When
, there are at most three induced overfull subgraphs, and it is possible to find an overfull subgraph in polynomial time. When 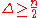 , there is at most one induced overfull subgraph, and it is possible to find it in linear time.
, there is at most one induced overfull subgraph, and it is possible to find it in linear time.

