Ovoid (projective geometry)
Encyclopedia
In PG, with q a prime power greater than 2, an ovoid is a set of 
points, no three of which collinear (the maximum size of such a set). When 
the largest set of non-collinear points has size eight and is the complement of a plane.
An important example of an ovoid in any finite projective three-dimensional space are the
points of an elliptic quadric (all of which are projectively equivalent).
When q is odd or
, no ovoids exist other than the elliptic quadric
s.
When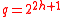
another type of ovoid can be constructed : the Tits
ovoid, also known as the Suzuki
ovoid. It is conjectured that no other ovoids exist in PG(3,q).
Through every point P on the ovoid, there are exactly
tangents, and it can be proven that these lines are exactly the lines through P in one specific plane through P. This means that through every point P in the ovoid, there is a unique plane intersecting the ovoid in exactly one point. Also, if q is odd or 
every plane which is not a tangent plane meets the ovoid in a conic
.
points, no three of which collinear (the maximum size of such a set). When the largest set of non-collinear points has size eight and is the complement of a plane.An important example of an ovoid in any finite projective three-dimensional space are the
points of an elliptic quadric (all of which are projectively equivalent).When q is odd or
, no ovoids exist other than the elliptic quadricQuadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
s.
When
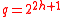another type of ovoid can be constructed : the TitsJacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
ovoid, also known as the Suzuki
Michio Suzuki
was a Japanese mathematician who studied group theory.-Biography:He was a Professor at the University of Illinois at Urbana-Champaign from 1953 to his death. He also had visiting positions at the University of Chicago , the Institute for Advanced Study , the University of Tokyo , and the...
ovoid. It is conjectured that no other ovoids exist in PG(3,q).
Through every point P on the ovoid, there are exactly
tangents, and it can be proven that these lines are exactly the lines through P in one specific plane through P. This means that through every point P in the ovoid, there is a unique plane intersecting the ovoid in exactly one point. Also, if q is odd or every plane which is not a tangent plane meets the ovoid in a conicConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
.